Système M/M/ 

Processus de naissance et de mort en équilibre

Sauf dans les cas très simples, il est impossible de résoudre les équations différentielles caractérisant un processus de naissance et de mort et, donc, de trouver une expression close pour 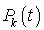 . Nous nous bornons ici à une étude de la distribution stationnaire lorsqu'elle existe. Partons donc de l'hypothèse suivante :

 .

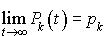On doit alors avoir :

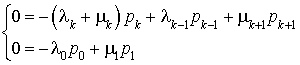
Ce système d'équations et 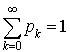  permettent de trouver la distribution stationnaire  .

Interprétation intuitive

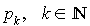Considérons les liens suivants entre l'état 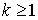E_k et les états voisins E_k-1 (qui existe pour  ) et E_k+1 dans le diagramme de transition :

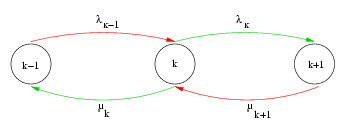
• Flux de probabilité vers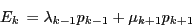  

• Flux de probabilité sortant de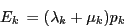  

Or, la condition d'équilibre implique :

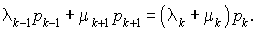
Cette équation reste valable pour 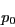et 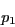, si l'on pose  .

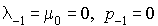Pour résoudre ce système d'équations, nous les mettons sous la forme suivante :

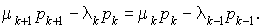
Il en résulte que

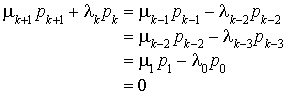
On en déduit 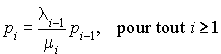   et, donc :

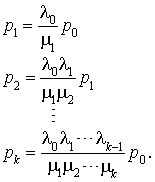
Puisque la somme des probabilité est égale à 1, on aura :

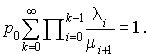
Cette dernière équation permet de trouver une expression pour p₀ et donc pour p_k, par les équations ci-dessus.

Condition d'existence d'équilibre

Remarquons d'abord que 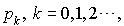  ne peut être une distribution de probabilité que si la série  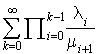 converge. Cette condition est donc une condition nécessaire pour l'existence d'une distribution stationnaire. Soient :

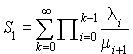
et

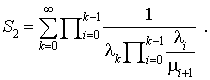
On démontre que tous les états du processus sont :

• ergodiques si et seulement si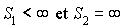  

• récurrents si et seulement si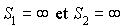  

• transitoires si et seulement si  .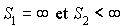

C'est le premier cas qui nous intéresse. Une condition suffisante pour l'ergodicité des états d'un processus de naissance et de mort est que 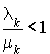 , lorsque k est assez grand. Pour une preuve complète voir [4].

Exercices