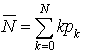Les systèmes que nous avons considérés jusque là étaient tous ouverts dans la mesure où le nombre d'usagers potentiels était supposé non borné. Or, il y a des situations réelles dans lesquelles le système n'est pas ouvert à tout le monde et les usagers potentiels sont fixés une fois pour toute. Dans cette condition, il est normal qu'on suppose que le taux d'arrivée est proportionnel au nombre de clients potentiels qui sont encore à l'extérieur du système. Les systèmes d'attente soumis à cette contrainte sont appelés systèmes fermés.
Considérons un système fermé avec N usagers potentiels, s serveurs identiques, chacun de taux de service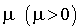 
. Si, à l'instant t, le nombre d'usagers dans le système est 
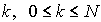, le taux d'arrivée est de 
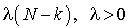, puisque le nombre d'usagers potentiels qui peuvent le joindre pour un service est
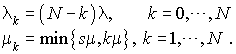
On peut supposer que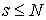 
sans perte de généralité. En effet, le taux de service ne peut pas dépasser 
.
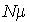Nous avons le diagramme de transition suivant :
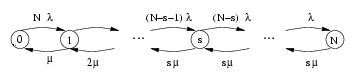
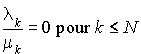. Nous avons alors :
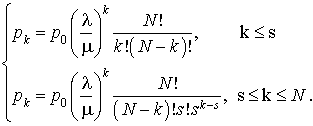
On en déduit
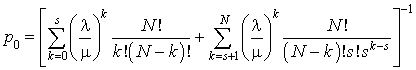
Pour le nombre moyen d'usagers en attente, nous avons :
