De nombreux systèmes d'attente peuvent être modélisés par un processus de naissance et de mort. Ces systèmes ont comme particularités communes un processus d'arrivée de type poissonnien et une durée de service suivant une loi exponentielle. On pourra avoir un nombre quelconque de serveurs. Le système peut adopter une discipline fixée sur la nature prioritaire d'ordre de service. Finalement, le système peut admettre un nombre fini ou infini d'usagers au total.
Un système d'attente est caractérisé par la notation de Kendall
X représente le processus d'arrivée; il peut être soit M lorsque le processus est de Poisson, D lorsqu'il est déterministe, ou G lorsqu'il est quelconque.
Y représente la loi de la durée de service; il peut être soit M pour la v.a. exponentielle, D pour une durée déterministe, ou G pour une durée de type général.
s est le nombre de serveurs, qui est un entier positif.
K est le nombre total d'usagers que le système peut admettre suivant des contraintes d'espace et d'accueil. Dans le cas où il est absent, ce nombre n'est pas limité.
La notation peut inclure aussi la discipline de service :
Le processus d'arrivée d'usagers est de Poisson de taux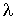 
et la durée de service est exponentielle de paramètre 
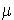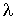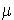. On suppose et strictement positifs. 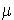est appelé taux de service. L'espérance mathématique de la durée de service est l'inverse du taux de service. Le processus se modélise par un processus de naissance et de mort avec :
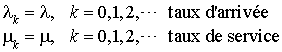
Nous avons le diagramme de transition suivant :
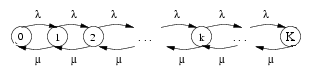
Suivant les résultats de la séquence précédente, le processus est ergodique si et seulement si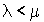 
, i.e. le taux de service est supérieur à celui d'arrivée, et les équations sur les probabilités stationnaires deviennent alors :
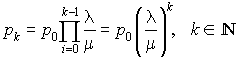
Par ailleurs, la somme des probabilités vaut 1, et donc :
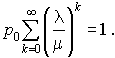
Par conséquent :
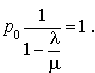
D'où
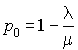
et
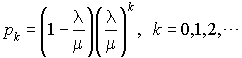
Soit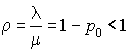 
. C'est la probabilité stationnaire pour que le système soit occupé. 
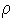est appelé taux d'occupation ou facteur d'utilisation du système.
La distribution stationnaire s'écrit alors :
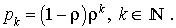
C'est une distribution géométrique. Elle possède la propriété caractéristique « sans mémoire » ; si N est la v.a. nombre d'usagers dans le système, on a :
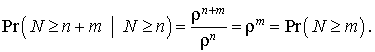
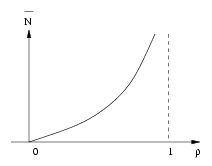
Le nombre d'usagers dans le système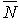 
vaut :
On a la courbe variation suivante pour 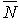en fonction de 
.
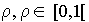Le temps passé par usager dans le système est par définition la somme de temps d'attente passé dans la file et celui du service. C'est une v.a. qui dépend évidemment de la discipline imposée. Mais le temps moyen d'attante par usager est indépendant de la discipline.
Considérons un intervalle de temps 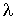avec le ratio entre le nombre d'usagers, passés dans le système, et la longueur de l'intervalle L. Soit N(t), pour 
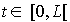, le nombre d'usagers dans le système, à l'instant t.
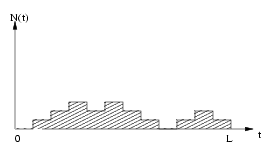
Soit A l'aire de la surface comprise entre la courbe de variation de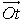 
. On a d'une part :
D'autre part cette aire est le produit du nombre total d'usagers, passés dans le système, et le temps moyen d'attente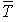 
. Comme ils sont arrivés de taux 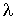, ce nombre vaut asymptotiquement 
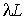. On a donc :
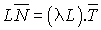où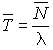 
.
C'est la formule de Little. Elle est valable dans tout système d'attente, si l'on peut identifier 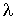avec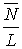 
.
Dans le cas du système
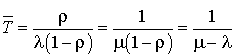
Le temps moyen passé dans la file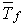 
est l'espérance mathématique du temps qu'un usager quelconque doit attendre dans la file (en régime stationnaire) pour être servi. Il vaut donc en général la différence entre 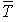et le temps moyen de service : 
.
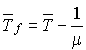Dans le cas du systéme 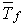. En effet, un usager qui vient d'arriver, trouve en moyenne 
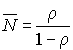usagers dans le système. Il doit donc attendre en moyenne :
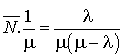
unités de temps pour être servi.
Notons que ceci est vrai en vertu de la propriété sans mémoire de la durée de service.