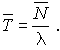Le processus d'arrivée est de Poisson de taux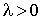 
, la durée de service une v.a. exponentielle de paramètre 
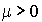et il y a s serveurs identiques. Le système précédent est un cas particulier de celui-ci.
Le processus de naissance et de mort modélisant le système admet le diagramme de transition suivant :
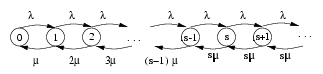
Donc :
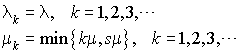
Le système admet une distribution stationnaire si et seulement si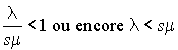 
; c'est-à-dire si le taux d'arrivée est inférieur au taux total de service. Supposons donc que cette condition est remplie et posons 
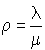. Nous avons :
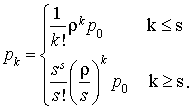
La somme des probabilités vaut 1 et, donc :
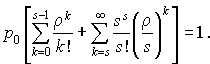
On en déduit :
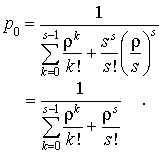
Le nombre moyen d'usagers (en régime stationnaire) vaut :
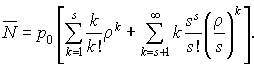
Par ailleurs, on a :
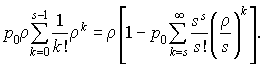
D'où :
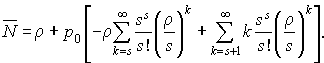
La première somme vaut :
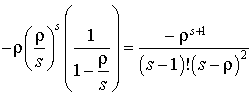
et la seconde :
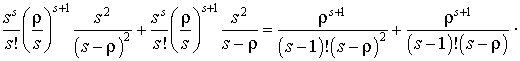
D'où :
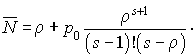
Le temps moyen passé par usager dans le système vaut
