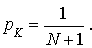Le système a un seul serveur. Le nombre total d'usagers dans le système ne peut pas dépasser K.
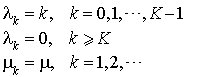
On suppose 
. Le système admet une distribution stationnaire, puisque 
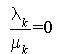pour
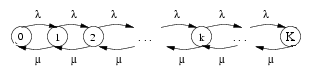
On a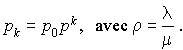 
Supposons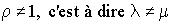 
. Nous avons :
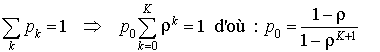
Et donc :
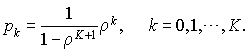
Le nombre moyen d'usagers dans le système vaut :
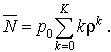
La probabilité pour qu'un usager, venant d'arriver, soit rejeté vaut en régime stationnaire :
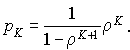
Ce nombre est la portion d'usagers perdus.
Pour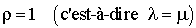 
, les expressions trouvées pour 
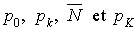ne sont pas valables (division par 0). Dans ce cas, nous aurons 
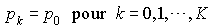. D'où 
.
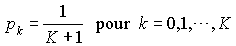On en déduit facilement :
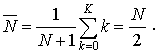
La portion d'usagers perdus vaut :
