Il y a une infinité de serveurs identiques :
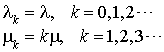
On suppose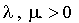 
.
Le système admet une distribution stationnaire. En effet, le rapport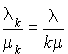 
devient inférieur à 1 dès que k dépasse 
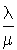. Nous avons alors :
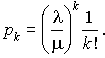
D'où
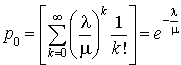
et
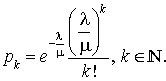
La distribution stationnaire est une distribution de Poisson. On en déduit :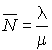 
.
Et donc, par la formule de Little,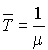 
.
Nous aurions pu obtenir ce dernier résultat sans aucun calcul, puisque le temps passé dans le système est le temps de service, qui est une v.a. exponentielle d'espérance mathématique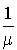 
.
