Système M/M/ 

Critère d'applicabilité des modèles markoviens

Les modèles proposés dans la séquence précédente étaient tous fondés par les postulats que le processus d'arrivée est de Poisson, et que la durée de service est une v.a. exponentielle. Ces hypothèses sont loin d'être universelles. On peut en effet considérer des circonstances où les arrivées suivent d'autres « motifs » que celui de Poisson ou les durées de service ne sont pas de type v.a. exponentielle.

Une question qui se pose est comment savoir si la modélisation convient ou non dans une circonstance donnée. Un autre problème soulevé est de déterminer, lorsque la réponse à la question précédente est positive, les paramètres (taux d'arrivée et taux de service) du processus. Des techniques statistiques nous permettent de fournir des solutions satisfaisantes à la problématique de cohérence de modélisation. Ces techniques sont fondées sur la vraisemblance entre le modèle théorique et l'observation effectuée pendant une certaine durée de temps.

Les exemples suivants sont tirés du livre « Eléments de la Recherche Opérationnelle », par Robert Faure, Gauthier-Villars Editeur. Ils illustrent une application d'un test statistique de 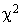  pour répondre aux problèmes posés par la modélisation du processus d'arrivée par un processus de Poisson et par l'identification de la durée de service par une v.a. exponentielle.

Dans une usine existe un bureau de la Sécurité Sociale, auquel les ouvriers ont accès pendant les heures de travail. Le chef du personnel, qui a remarqué l'affluence des intéressés au guichet, demande qu'une étude relative au fonctionnement de ce service lui soit présentée.

Un analyste est désigné pour déterminer le temps moyen d'attente des ouvriers dans la file et la durée moyenne de l'entretien que chacun a avec le préposé, lors du dépôt des dossiers de maladie.

Il s'agit bien d'un problème d'attente à une station.

Le premier travail de l'analyste sera de définir les périodes pendant lesquelles le phénomène peut être considéré comme stationnaire : durant la première demi-heure et la dernière de la journée, ainsi que l'heure du repas, l'affluence au guichet est très fluctuante et faible; au contraire, durant les autres périodes de la journée, le phénomène stationnaire est établi et l'on peut songer à examiner les entrées et services du point de vue statistique.

Etude des arrivées

Pendant cent intervalles de cinq minutes, successifs ou non, mais tous situés dans la période de stationnarité, le nombre de « clients » arrivant durant chaque intervalle de cinq minutes est décompté.

Supposons que les résultats soient les suivants :

La moyenne de cette loi de distribution est facile à calculer :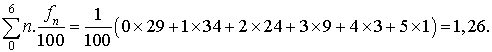  

L'emploi d'un test statistique va permettre de vérifier si la loi observée se rapproche d'une loi théorique classique, en l'espèce de celle de Poisson. La formule :

  ,

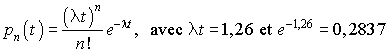permet de calculer les fréquences théoriques d'une loi de Poisson de moyenne 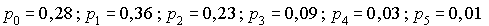1,26 ; ce sont cent fois les valeurs :   (cette dernière probabilité est en réalité la différence entre 1 et la somme des autres  ).

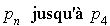Employons, par exemple, le test du 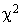  de Pearson, qui s'applique à des classes dans lesquelles le nombre d'événements attendus est de l'ordre de 5 (il nous suffira de regrouper les deux dernières classes pour satisfaire grossièrement à cette exigence).

Ce test consiste à calculer les carrés des différences entre les fréquences théoriques de la loi à vérifier et les fréquences observées, puis à diviser chacun de ces carrés par la fréquence théorique de la classe à laquelle les fréquences sont relatives.

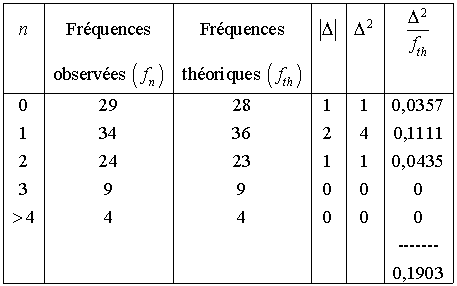
Le nombre de degrés de liberté du système est d = c - 1 - p, c étant le nombre de classes (ici : 5) et p le nombre de paramètres de la loi théorique tirés de l'observation (ici : 1, la moyenne); on a donc : d= 5 - 1 - 1 = 3.

Or, en se reportant à une table des 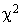 , on trouve, pour 3 degrés de liberté :  .

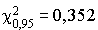Comme le 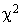 calculé (0,19) est inférieur à cette valeur, l'analyste décide d'admettre que le phénomène observé suit une loi de Poisson (en réalité, le test signifie que, si l'hypothèse était exacte, pour 95 % des échantillons, la valeur  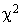 serait inférieure à 0,352 ; le risque de rejeter l'hypothèse, alors qu'elle est exacte, si le  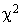 calculé est supérieur au  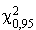 relevé dans la table, n'est que de 5 %).

La conclusion à tirer de l'étude des arrivées est qu'elles se font « à la Poisson », avec un taux de 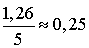  arrivée par minute.

Etude des services

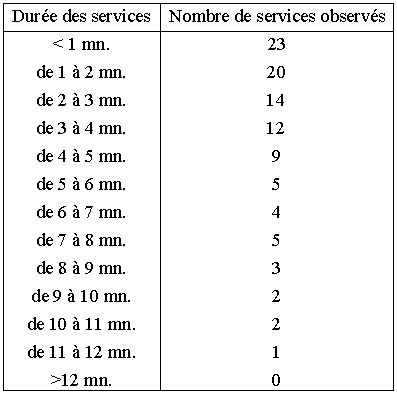
A cent reprises, consécutives ou non, mais prises dans la période stationnaire, on relève la durée du service, c'est-à-dire le temps passé par un client au guichet.

Supposons que les résultats obtenus soient les suivants :

La moyenne est ici :

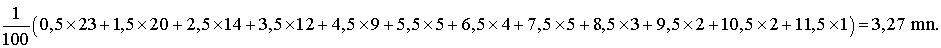
Le nombre de clients servis par minute est donc :

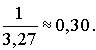
On fait alors l'hypothèse que la loi des services est une loi exponentielle de taux  .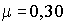

En réduisant à neuf classes et sept degrés de liberté, on a 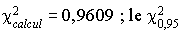 , lu dans la table, s'élève à 2,167 et l'analyste décide d'admettre qu'il a bien une loi exponentielle de taux  .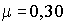