Chacun de ces produits demande, pour son usinage, des heures de fabrication unitaires sur les machines (ou dans les ateliers) A B C D E comme indiqué dans le tableau suivant :
| A | B | C | D | E | |
| P1 | 0 | 1h,5 | 2 | 3 | 3 |
| P2 | 3 | 4 | 3 | 2 | 0 |
| Disponibilité totale de chaque machine | 39h | 60h | 57h | 70h | 57h |
Les marges brutes de chaque produit sont respectivement :
M1 = 1 700 F
M2 = 3 200 F
Ecrire un programme linéaire correspondant.
Les produits utilisent trois fournitures F1, F2 et F3 dans les conditions indiquées ci-dessous :
| F1 | F2 | F3 | |
| P1 | 0 | 12 | 8 |
| P2 | 5 | 36 | 0 |
| Unités | Kg | M³ | M² |
| Stock disponible | 55 | 432 | 126 |
Réécrire sous forme algébrique seulement, le nouveau programme
linéaire ainsi créé. Eliminer les contraintes redondantes.
Cliquez pour afficher la réponse correspondante (réponse ).
).
Exemple 2 :Composition d’Aliments pour le Bétail.
On désire déterminer la composition, à coût minimal, d’un aliment pour bétail qui est obtenu en mélangeant au plus trois produits bruts : orge, arachide, sésame. L’aliment ainsi conditionné devra comporter au moins 22% de protéines et 3,6% de graisses, pour se conformer aux exigences de la clientèle. On a indiqué ci-dessous les pourcentages de protéines et de graisses contenus, respectivement, dans l’orge, les arachides et le sésame, ainsi que le coût par tonne de chacun des produits bruts :
| Produit brut | 1 |
2 |
3 |
Pourcentage requis |
| ORGE | ARACHIDES | SESAME | ||
| Pourcentage de protéines | 12% | 52% | 42% | 22% |
| Pourcentage de graisses | 2% | 2% | 10% | 3,6% |
| coût par tonne | 25 | 41 | 39 |
- On notera Xj (j = 1, 2, 3) la fraction de tonne de produit brut j contenu dans une tonne d’aliment. Formuler le problème algébriquement.
- Montrer qu’il est possible de réduire la dimension du problème.
Cliquez pour afficher la réponse correspondante (réponse ).
).
Un fabricant désire produire 100 Kg d’une préparation de base pour crème glacée. Cette préparation doit contenir 21,5 Kg de matières grasses, 21 Kg de sucre, 1,2 Kg d’œuf et 53 Kg d’eau. Les ingrédients dont il dispose figurent en tête des colonnes du tableau ci-dessous ; les constituants figurent en ligne. Ce tableau précise également les pourcentages (en poids) de chaque constituant dans chaque ingrédient ainsi que le coût, au Kg, de chaque ingrédient.
Ingrédients |
|||||||
| Crème | Jaune d'oeuf frais | Lait entier en poudre | Jaune d'oeuf surgelé et sucré | Sirop de sucre de canne | eau | ||
| Constituants | Matières grasses | 40 | 50 | 12 | 30 | ||
| Sucre | 14 | 70 | |||||
| Oeuf | 40 | 40 | |||||
| Eau | 60 | 10 | 88 | 16 | 30 | 100 | |
| Coût en Kg | 3 F | 4 F | 1 F | 2 F | 0,80 F | 0,00 F | |
- Le fabricant désire déterminer la composition du mélange de coût minimal. Ecrire le programme linéaire correspondant à ce problème, sans le résoudre.
-
Jusqu’à présent, le fabricant produisait le mélange suivant :
Quel est le coût de ce mélange ? Peut-on dresser le tableau du simplexe associé à cette solution ? Pourquoi ? Si oui, le faire.CREME 50 Kg JAUNE D'OEUF FRAIS 3 Kg SIROP 30 Kg EAU 17 Kg - Quelle est la composition du mélange de coût minimal ?
- Par suite de fluctuations économiques, les prix de la crème
et du jaune d’œuf frais passent respectivement à 4 et 7
F.
Le mélange déterminé à la question 3 est-il toujours de coût minimal ?
Cliquez pour afficher la réponse correspondante (réponse
 ).
).
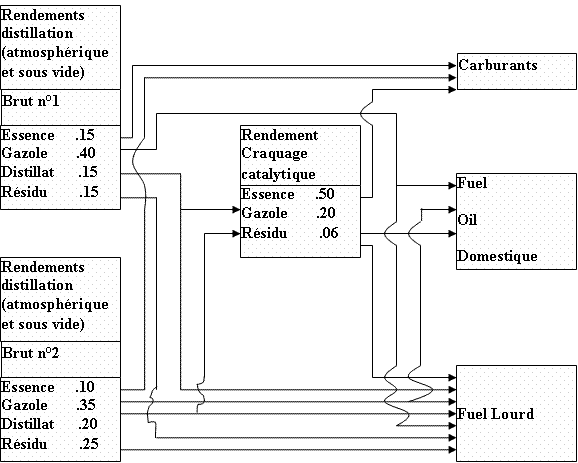
Exemple 4 :Schématisation d’une Raffinerie
Une raffinerie, représentée sur le schéma ci-dessous, dispose d’une unité de distillation (permettant d’obtenir quatre produits : carburants, gazole, distillat lourd, résidu), une unité de reformage et une unité de craquage catalytique (pouvant traiter les distillats lourds).
Pendant une période donnée, la raffinerie peut traiter deux pétroles bruts B1 et B2 dont les rendements sont indiqués sur le schéma (pour les carburants de rendements indiqués correspondent aux produits finis après passage par l’unité de reformage). Les prix de B1 et B2 sont respectivement de 1 300 F/t et de 1 500 F/t. Les frais de distillation sont estimés à 10 F/t. Le coût de traitement du distillat sous vide au craquage catalytique est de 20 F/t. On distingue seulement 3 types de produits : la raffinerie doit fabriquer pendant la période considérée, au moins, 200 000 t de carburants ; 400 000 t de fuel-oil domestique et 250 000 t de fuel lourd ; elle cherche à minimiser son coût de production.
Par ailleurs, les produits finis doivent satisfaire certaines contraintes de
qualités :
- la teneur en soufre du fuel-oil domestique doit être inférieure
à 0,5%, la teneur en soufre du gasoil issu de la distillation du brut
n°1 étant de 0,2% en poids et de 1,2% pour le brut n°2, la teneur
de gasoil de craquage étant de 0,3% en poids pour le brut n°1 et
de 2,5% en poids pour le brut n°2.
Enfin le raffineur doit traiter au moins 550 000 t de brut n°1 et la capacité
du craquage est de 200 000 t pour la période considérée.
Formuler le problème en terme de programmation linéaire ; on pourra donner un nom mnémonique aux variables.
Cliquez pour afficher la réponse correspondante (réponse ).
).
Un physicien ayant fait n expériences, s’est rendu compte qu’une
certaine quantité Q est fonction de la variable t. Il a de bonnes raisons
de penser que la loi reliant Q à t est de la forme :
Q(t) = a sin(t) + b tg(t) + c
,
où les paramètres a et b sont à choisir numériquement
« au ieux » à partir des n expériences réalisées
: celles –ci, pour n valeurs différentes de t: ![]() ,
, ![]() ,..., et
,..., et ![]() ont donné pour Q, les valeurs
ont donné pour Q, les valeurs ![]() ,
, ![]() ,...,
,..., ![]() .
.
Tenant compte du fait que ces n expériences sont entachées d’erreur
et que la loi prévue n’est peut-être qu’approximative,
le physicien n’espère pas trouver un ajustement parfait (le système
d’équations a sin(![]() ) + b tg(
) + b tg(![]() ) + c =
) + c = ![]() (i = 1, 2, …, n) aux inconnues a, b et c n’admet pas
de solution). Le physicien a deux idées différentes de ce qu’un
meilleur ajustement peut signifier :
(i = 1, 2, …, n) aux inconnues a, b et c n’admet pas
de solution). Le physicien a deux idées différentes de ce qu’un
meilleur ajustement peut signifier :
(1) la première idée consiste à chercher a, b, c minimisant
![]()
(2) La seconde idée consiste à chercher a, b, c minimisant :
![]()
Par ailleurs, et pour des raisons physiques, les coefficients a, b, c doivent
être supérieurs ou égaux à zéro.
Montrer que dans chacun des cas (1) et (2) on peut formuler le problème
comme un programme linéaire qu’on explicitera.
Cliquez pour afficher la réponse correspondante (réponse
 ).
).
 |