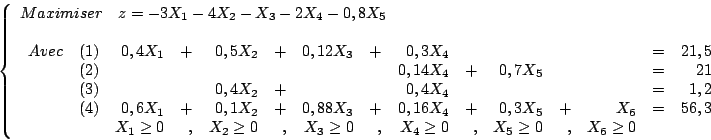
On constate que la solution proposée vérifie les contraintes
: elle est donc admissible. La valeur de la fonction économique pour
cette solution est de 186 F.
La matrice B correspondant aux variables non utiles ![]() ,
, ![]() ,
, ![]() ,
, ![]() est définie par :
est définie par :
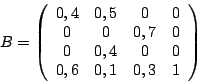
Comme son déterminant vaut -0,112, elle est inversible ; la solution
proposée est donc de base.
Partant d’une base initiale formée de variables artificielles,
en faisant successivement entrer les variables ![]() ,
, ![]() ,
, ![]() et
et ![]() dans la base (par exemple), on obtient le tableau du simplexe correspondant
à cette solution de base:
dans la base (par exemple), on obtient le tableau du simplexe correspondant
à cette solution de base:
| i | 1 | 2 | 3 | 4 | 5 | 6 | Ui | |||
| 1 | 1 | 0 | 0,3 | -0,5 | 0 | 0 | 50 | |||
| 2 | 0 | 1 | 0 | 1 | 0 | 0 | 3 | |||
| 5 | 0 | 0 | 0 | 0,2 | 1 | 0 | 30 | |||
| 6 | 0 | 0 | 0,7 | 0,3 | 0 | 1 | 17 | |||
| Dj | 0 | 0 | -0,1 | 0,66 | 0 | 0 | 186 | z | ||
Comme D4 est positif, la solution n’est pas optimale.
Une autre manière, plus rapide, d’obtenir ce tableau, consiste
à remarquer (sachant que la base consiste en ![]() ,
, ![]() ,
, ![]() et
et ![]() ) que
) que ![]() n’est pas présent dans (4) : cette équation
servira donc à exprimer
n’est pas présent dans (4) : cette équation
servira donc à exprimer ![]() ; puis (3) pour exprimer
; puis (3) pour exprimer ![]() , (2) pour
, (2) pour ![]() et enfin (1) pour
et enfin (1) pour ![]() .
.