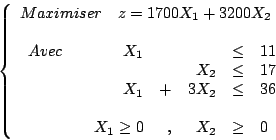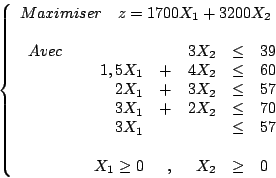
Solution de l'exercice 1
Formalisation du problème
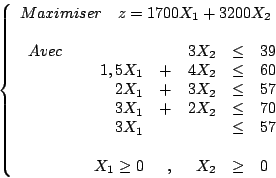
Le nouveau programme linéaire s'écrit:

La contrainte (1) entraine ![]() et la contrainte (6)
et la contrainte (6) ![]() .
.
La contrainte (1) est donc redondante.
De mème (5) entraine ![]() , mais (8) entraine
, mais (8) entraine ![]() .
.
Donc la contrainte (5) est redondante.
(2) s'écrit
![]() .
(7) s'écrit
.
(7) s'écrit
![]() .
.
La contrainte (2) est donc redondante.
(7) s'écrit (7'):
![]() .
(8) s'écrit
.
(8) s'écrit
![]() .
.
En les additionnant, on obtient
![]() .
La contrainte (3) est donc redondante.
(6) et (8) s'écrivent (6'):
.
La contrainte (3) est donc redondante.
(6) et (8) s'écrivent (6'): ![]() et (8'):
et (8'): ![]() .
Additionnons à (7') l'inégalité (6') et 5 fois l'inégalité (8').
On obtient
.
Additionnons à (7') l'inégalité (6') et 5 fois l'inégalité (8').
On obtient
![]()
![]() La contrainte (4) est donc redondante.
La contrainte (4) est donc redondante.
Le problème devient donc: