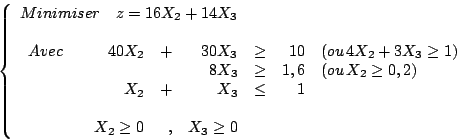Puisqu’il s’agit d’obtenir une tonne d’aliment,
en appelant respectivement, ![]() ,
, ![]() et
et ![]() les fractions d’orge, d’arachide et de sésame
dans la dite tonne, on doit avoir
les fractions d’orge, d’arachide et de sésame
dans la dite tonne, on doit avoir
![]() ,
qui sera une contrainte de notre problème.
,
qui sera une contrainte de notre problème.
Remarque : On peut parler soit en fraction de tonne, soit en pourcentage,
c’est équivalent.
Par ailleurs, l’aliment doit contenir au moins 22% de protéines.
D’où la contrainte :
![]() .
.
Et de même, pour les graisses, on doit avoir :
![]() .
.
D’autre part, comme on désire fabriquer le produit à
coût minimal, on devra minimiser la somme :
![]() .
.
Soit, en récapitulant, le programme linéaire :
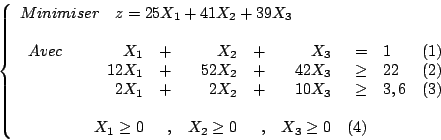
En tenant compte de la contrainte d’égalité, on remarque
qu’on peut réduire le nombre de variables du problème
en écrivant :
![]()
La fonction à optimiser devient alors
![]() .
.
Soit
![]()
Comme il s’agit de faire varier ![]() et X3, la constante 25 n’intervient pas et la fonction à
optimiser est:
et X3, la constante 25 n’intervient pas et la fonction à
optimiser est:
![]()
Sous les contraintes
![]()
![]()
![]() .
.
Mais, la contrainte ![]() =0 du problème initial ne saurait être omise, et elle
s’écrit alors :
=0 du problème initial ne saurait être omise, et elle
s’écrit alors :
![]() .
.
Soit aussi :
![]() .
.
Soit en récapitulant, le programme linéaire suivant :