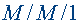avec découragementExercice 1 : Système 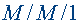avec découragement
On considère un système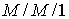 
où des usagers arrivent de taux variable proportionnel à l'inverse du nombre d'usagers dans le système : 
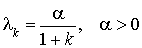. Le taux de service est 
.
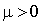Montrer que le système est ergodique. Ecrire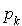 
en fonction de 
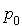et en déduire que la distribution stationnaire est une distribution de Poisson.
Trouver le nombre moyen d'usagers dans le système. Trouver la longueur moyenne de la file d'attente.
Trouver le taux moyen d'arrivée et en déduire, par la formule de Little, le temps moyen passé par usager dans le système.
Des camions arrivent dans une station service pour passer des tests de sécurité, suivant un processus de Poisson de taux de 6 / jour. La durée des tests pour chaque camion est une v.a exponentielle d'espérance mathématique de 1h 30 mn. On suppose que le processus d'arrivée ne s'interrompt pas et que la station travaille 24 heures sur 24.
Le système admet-il une distribution stationnaire ?
Si oui la calculer et donner le nombre moyen d'usagers dans le système, le temps moyen passé dans le système, la longueur moyenne de la file d'attente et le temps moyen passé dans la file (en régime stationnaire).
Deux lignes téléphoniques sont mises à la disposition des clients qui passent des commandes. Lorsque les deux lignes sont occupées les appels restent en file et dès qu'une ligne est libérée le premier entre en contact. On suppose que des appels arrivent suivant le processus de Poisson de taux de 30 à l'heure et l'on retient l'hypothèse que la durée de la commande est une v.a. exponentielle de durée moyenne 3 mn.
Dessiner le diagramme de transition. Le système est-il ergodique ? Si oui trouver la distribution stationnaire.
Trouver le nombre moyen d'appels branchés, le nombre moyen d'appels en attente, la durée moyenne de temps passé par usager et la durée d'attente pour avoir une conversation en régime stationnaire
Quelle est la portion de temps où les deux lignes sont occupées ?
Une entreprise de construction possède deux engins identiques, chacun pouvant tomber en panne indépendamment de l'autre suivant un processus de Poisson de taux 5 fois par mois. On suppose que la durée de réparation est une v.a. qui suit une loi exponentielle de paramètre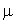 
(taux de service). Pour quelle valeur de 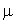, les deux engins seront-ils simultanément en état de marche au moins la moitié du temps ?
Une blanchisserie possède 3 machines identiques et indépendantes. Chaque machine a une durée de fonctionnement indépendante du passé, suivant une loi exponentielle d'espérance de deux jours. Une machine qui tombe en panne est réparée par un technicien ; la durée de réparation est une v.a. d'espérance d'un jour. La blanchisserie n'a qu'un technicien.
Dessiner le diagramme de transition.
Quelle est la fraction de temps où toutes les machines fonctionnent et celle où toutes les machines sont hors service ?
Quel est le nombre moyen de machines en état de marche ? Quel est le nombre moyen de machines immobilisées ?
Dans une entreprise de service, où les usagers arrivent suivant un processus de Poisson de taux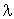 
( 
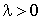), la direction a le choix entre 3 modèles suivants.
Installation d'un serveur dont la durée de service suit une loi exponentielle de paramètre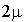 
.
Installation de 2 serveurs séparés et identiques, chacun admettant une durée de service suivant une loi exponentielle de paramètre 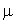. Tout usager venant d'arriver, choisit, avec la probabilité 
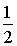l'un des serveurs et il n'y a pas d'échange d'usagers potentiels chez les serveurs.
Installation de deux serveurs (identique au modèle B) non séparés. Dès que l'un des serveurs est libre, s'il y a des usagers en attente le premier arrivé se fait servir chez le serveur libéré.
On suppose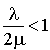 
.
Calculer le temps moyen passé dans le système. Lequel des 3 systèmes est le plus performant ?
Peut-on répondre à la question précédente sans faire le calcul de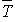 
?
 |
Consulter la solution...