Module C1.7 : Processus stochastique et simulation
Description d'un processus de Poisson
Exercices
Exercice 1 :
Montrer que la somme de deux processus indépendants de Poisson de taux respectifs 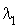 et
et 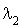 est un processus de Poisson de taux
est un processus de Poisson de taux 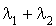 .
.
Réciproquement : soit  une source d'usagers qui est un processus de Poisson de taux
une source d'usagers qui est un processus de Poisson de taux 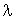 ; soit la somme de
; soit la somme de 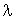 sources indépendantes
sources indépendantes 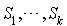 . On suppose que la probabilité pour qu'un usager quelconque de
. On suppose que la probabilité pour qu'un usager quelconque de  soit originaire de
soit originaire de 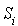 est
est 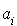 , avec
, avec 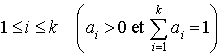 . Montrer que chaque source
. Montrer que chaque source 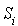 d'usagers est un processus de Poisson de taux
d'usagers est un processus de Poisson de taux 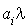 .
.
 Consulter la solution...
Consulter la solution...
Exercice 2 :
On considère deux processus de Poisson 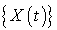 et
et 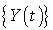 indépendants de taux
indépendants de taux 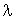 et
et  respectivement. Posons :
respectivement. Posons : 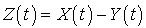 .
.
Le processus 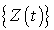 n'est pas poissonnien. Pourquoi ?
n'est pas poissonnien. Pourquoi ?
Donner une caractéristique de 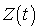 par sa fonction génératrice :
par sa fonction génératrice :
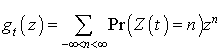
En déduire l'espérance mathématique et la variance de 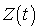 .
.
On associe à ce problème la situation d'une station de taxis, où 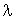 est le taux d'arrivée de passagers et
est le taux d'arrivée de passagers et  celui de taxis. Que peut-on dire de
celui de taxis. Que peut-on dire de 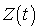 ?
?
 Consulter la solution...
Consulter la solution...
Exercice 3 (arrivées par paquets) :
Considérons un système d'arrivées d'usagers, où les clients arrivent à plusieurs. Des « paquets » d'usagers arrivent suivant un processus de Poisson de taux 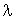 , mais chaque arrivée contient un nombre aléatoire de clients (indépendamment des autres).
, mais chaque arrivée contient un nombre aléatoire de clients (indépendamment des autres).
Etudier le nombre total d'usagers passés dans le système via une fonction génératrice dans les cas suivants :
Chaque arrivée contient un nombre aléatoire qui suit une loi de Poisson de paramètre 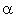 .
.
Chaque arrivée contient un nombre aléatoire qui suit une loi binomiale de paramètres 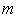 et
et 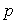 .
.
 Consulter la solution...
Consulter la solution...
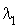 et
et 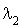 est un processus de Poisson de taux
est un processus de Poisson de taux 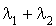 .
. une source d'usagers qui est un processus de Poisson de taux
une source d'usagers qui est un processus de Poisson de taux 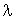 ; soit la somme de
; soit la somme de 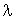 sources indépendantes
sources indépendantes 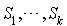 . On suppose que la probabilité pour qu'un usager quelconque de
. On suppose que la probabilité pour qu'un usager quelconque de  soit originaire de
soit originaire de 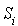 est
est 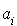 , avec
, avec 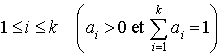 . Montrer que chaque source
. Montrer que chaque source 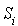 d'usagers est un processus de Poisson de taux
d'usagers est un processus de Poisson de taux 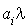 .
. Consulter la solution...
Consulter la solution...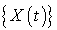 et
et 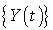 indépendants de taux
indépendants de taux  respectivement. Posons :
respectivement. Posons : 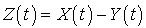 .
.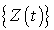 n'est pas poissonnien. Pourquoi ?
n'est pas poissonnien. Pourquoi ?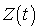 par sa fonction génératrice :
par sa fonction génératrice :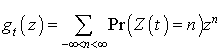
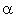 .
.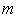 et
et 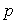 .
.