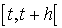 un intervalle de temps. La probabilité d'une arrivée dans le processus résultant vaut :
un intervalle de temps. La probabilité d'une arrivée dans le processus résultant vaut :Solution de l'exercice 1
a. Soit 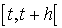 un intervalle de temps. La probabilité d'une arrivée dans le processus résultant vaut :
un intervalle de temps. La probabilité d'une arrivée dans le processus résultant vaut :
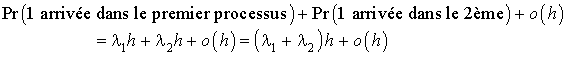
Cette probabilité ne dépend pas des événements précédant l'instant 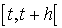 . On en déduit que le processus résultant est un processus de Poisson de taux
. On en déduit que le processus résultant est un processus de Poisson de taux 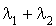 .
.
Une autre méthode pour démontrer cette proposition est la propriété bien connue que la somme des v.a. indépendantes de Poisson de paramètres 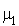 et
et 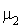 est une v.a. de Poisson de paramètre
est une v.a. de Poisson de paramètre 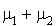 . Ainsi, si
. Ainsi, si 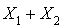 est le nombre total d'arrivées dans l'intervalle
est le nombre total d'arrivées dans l'intervalle 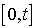 , on a :
, on a :
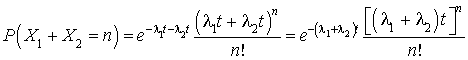
b. Réciproquement :
Considérons un intervalle de temps 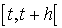 et calculons la probabilité pour qu'une arrivée ait eu lieu dans
et calculons la probabilité pour qu'une arrivée ait eu lieu dans 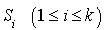 pendant cet intervalle.
pendant cet intervalle.
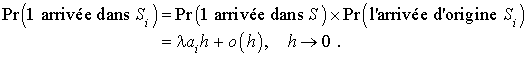
Le terme 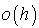 correspond aux probabilités de plus d'une arrivée dans
correspond aux probabilités de plus d'une arrivée dans  . Le processus d'arrivées dans
. Le processus d'arrivées dans 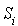 est donc bien de Poisson de taux
est donc bien de Poisson de taux 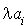 .
.
Il existe une autre démonstration fondée sur le calcul de 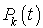 pour la source
pour la source 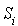 .
.
 |