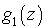 est la fonction génératrice du nombre d'usagers dans une seule arrivée, on a :
est la fonction génératrice du nombre d'usagers dans une seule arrivée, on a :Solution de l'exercice 3
a. Dans le premier cas, si 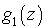 est la fonction génératrice du nombre d'usagers dans une seule arrivée, on a :
est la fonction génératrice du nombre d'usagers dans une seule arrivée, on a :
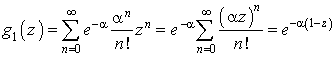
On en déduit la fonction génératrice associée au nombre d'usagers dans 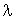 arrivées :
arrivées :
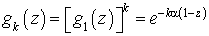
Par ailleurs, la probabilité d'avoir 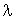 arrivées dans l'intervalle
arrivées dans l'intervalle 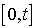 vaut
vaut 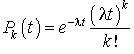 . D'où la fonction génératrice du nombre d'usagers est données par :
. D'où la fonction génératrice du nombre d'usagers est données par :
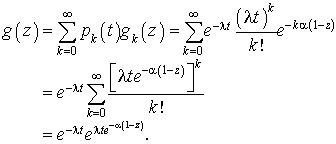
On peut facilement en déduire l'espérance mathématiques et la variance du nombre d'usagers passés dans le système dans 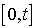 .
.
Si 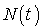 désigne le nombre d'usagers passés dans le système dans
désigne le nombre d'usagers passés dans le système dans 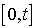 , un calcul simple fondé sur des dérivations (cf. exercice 2) aboutit à :
, un calcul simple fondé sur des dérivations (cf. exercice 2) aboutit à :
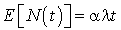 et
et 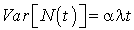
b. Dans le deuxième cas, avec les mêmes notations pour les fonctions génératrices nous avons :
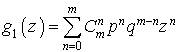 où
où 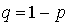 .
.
Donc 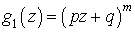 .
.
Un raisonnement analogue au cas précédent conduit à :
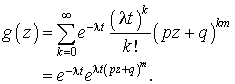
Avec un calcul similaire au calcul du cas précédent, nous aurons :
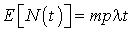 et
et 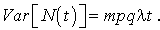
 |