 , où
, où Qu'est-ce qu'un processus de Poisson ?
Beaucoup de phénomènes physiques peuvent être raisonnablement modélisés par des processus de Poisson. Ces processus stochastiques  , où
, où

Pour des raisons que nous allons voir dans la suite, une incrémentation est appelée arrivée. Ces processus sont soumis à des postulats qui régissent les comportements aléatoires des occurences de nombreux phénomènes naturels. Il est aisé de désigner 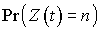 par
par 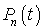 et, donc,
et, donc, 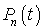 est la probabilité d'avoir n arrivées dans l'intervalle de temps
est la probabilité d'avoir n arrivées dans l'intervalle de temps
Divisons l'intervalle unitaire 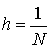 .
.

Soit I l'un des sous-intervalles. On a :

Par conséquent, le nombre moyen de sous-intervalles ayant reçu une incrémentation vaut :
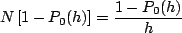
Lorsqu'on impose l'impossibilité de simultanéité de plusieurs arrivées, si h tend vers 0, alors  tend vers le nombre moyen de sauts dans un intervalle unitaire.
tend vers le nombre moyen de sauts dans un intervalle unitaire.
Supposons alors que cette limite existe et vaille 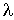 , on a alors :
, on a alors :
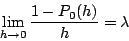
Donc, pour  :
:
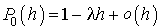
ou :
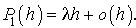
Un processus stochastique  avec le temps continu et la variable aléatoire discrète, prenant ses valeurs dans N, est un processus de Poisson, si :
avec le temps continu et la variable aléatoire discrète, prenant ses valeurs dans N, est un processus de Poisson, si :
Le processus commence à l'instant 0 avec l'état
La seule transition directe admise est la transition 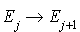 de l'état j vers l'état
de l'état j vers l'état
A tout instant t, la probabilité d'une arrivée dans l'intervalle 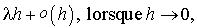 et ceci quel que soit l'évolution du processus avant l'instant t et l'état du système à cet instant.
et ceci quel que soit l'évolution du processus avant l'instant t et l'état du système à cet instant.
On appelle 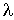 paramètre du processus ou taux d'arrivée. Le théorème suivant caractérise entièrement le nombre d'arrivées dans un intervalle de temps donné.
paramètre du processus ou taux d'arrivée. Le théorème suivant caractérise entièrement le nombre d'arrivées dans un intervalle de temps donné.
Théorème 1 Soit On a : c'est-à-dire que le nombre d'arrivées dans |
Pour simplifier la preuve de ce théorème central, nous montrons d'abord le lemme suivant :
Lemme 1 Pour le processus de Poisson du théorème 1, nous avons le système d'équations différentielles :
|
Démonstration. Considérons deux instant t et
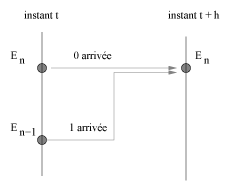
On a :
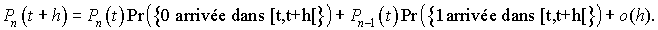
En effet, le premier terme du second membre est la probabilité d'avoir n arrivées jusqu'à l'instant t et 0 arrivées dans l'intervalle
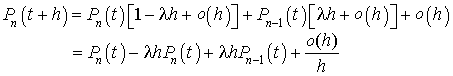
On en déduit : 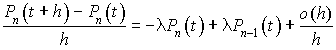 .
.
Comme 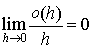 , on obtient :
, on obtient : 
Revenons maintenant à la preuve du théorème 1 que l'on obtient en faisant un raisonnement par récurrence.
Démonstration.
D'après le lemme précédent, on a :
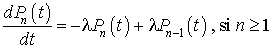
Dans le cas où  , le terme
, le terme 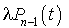 disparaît, puisque la transition
disparaît, puisque la transition  de la preuve du lemme n'existe pas. Donc, pour
de la preuve du lemme n'existe pas. Donc, pour  on peut écrire :
on peut écrire :
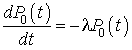
Ces deux équations différentielles constituent un système d'équations dont la solution est  , lorsqu'on, impose la condition initiale (1) du processus de Poisson.
, lorsqu'on, impose la condition initiale (1) du processus de Poisson.
Pour  , l'équation différentielle admet la solution générale :
, l'équation différentielle admet la solution générale :
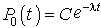
Mais 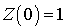 avec la probabilité 1 et, donc,
avec la probabilité 1 et, donc, 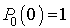 . D'où
. D'où 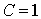 et :
et :
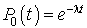
L'équation  est donc valable pour
est donc valable pour  .
.
Montrons maintenant que si elle est vraie pour n elle est vraie pour  .
.
Considérons donc l'équation 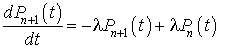 et posons
et posons  . Il vient
. Il vient  .
.
C'est une équation linéaire avec second membre. On peut utiliser la méthode de variation de constante pour la résoudre. L'équation sans second membre admet la solution 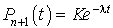 . On pose alors
. On pose alors 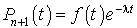 , en reportant dans l'équation avec second membre ci-dessus, on obtient après les simplifications nécessaires
, en reportant dans l'équation avec second membre ci-dessus, on obtient après les simplifications nécessaires 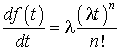 , ce qui admet la solution
, ce qui admet la solution 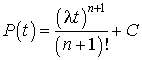 . D'où :
. D'où :
 .
.
Tenant compte de la condition initiale 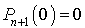 , on obtient
, on obtient 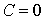 et donc :
et donc :

Le nombre d'arrivées dans un intervalle de temps de durée t dans un processus de Poisson de taux 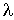 suit donc une loi de Poisson de paramètre
suit donc une loi de Poisson de paramètre 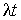 ; on en déduit :
; on en déduit :
L'espérance mathématique de 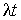 .
.
La variance de 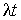 .
.
La fonction génératrice de 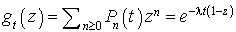 .
.
Un calcul simple établit les propriétés ci-dessus (voir aussi [4]).
La réciproque du théorème est aussi vraie :
Proposition 1 Si le nombre d'arrivées dans tout intervalle de temps de durée t suit, indépendamment du passé, une loi de Poisson de paramètre proportionnel à la durée t, alors le processus d'arrivées est un processus de poisson dont le taux d'arrivée est le coefficient de proportionnalité. |
Démonstration : Le processus démarre avec l'état 0. On a :

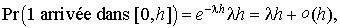

entraînant que les 3 postulats des processus de Poisson sont respectés.
Questionnaire de compréhension immédiate