



suivant: Concepts et notations ensemblistes
monter: Fondements
précédent: Exercices
Table des matières
Index
Notations
Dans ce chapitre, nous introduisons un certain nombre de
concepts et de notations qui ne sont peut-être pas connus du
lecteur. Par concept, il faut comprendre un nom pour une
entité non encore nommée, tandis que notation signifie un
symbole avec une signification particulière.
La plupart du temps, ces concepts et notations semblent plus
compliqués qu'ils ne le sont réellement. Diverses raisons peuvent
conduire à l'introduction d'une notation pour un concept :
- elle évitera la répétition de phrases assez longues à chaque
référence au concept,
- elle permet d'être plus précis qu'une phrase de texte, souvent ambiguë,
- elle devient langage international puisqu'elle remplace par une entité simple
une phrase d'une langue naturelle particulière.
Prenons quelques exemples a priori bien connus par le lecteur.
Exemples :
- La racine carrée d'un nombre
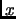 supérieur ou égal à zéro
est un nombre positif tel qu'en le multipliant par lui-même, on
obtient exactement le nombre
supérieur ou égal à zéro
est un nombre positif tel qu'en le multipliant par lui-même, on
obtient exactement le nombre 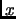 . La notation est
. La notation est 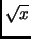 . Supposons
que nous souhaitions exprimer la relation
. Supposons
que nous souhaitions exprimer la relation
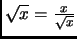 , mais n'ayons le droit d'utiliser ni la notation
, mais n'ayons le droit d'utiliser ni la notation
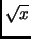 ni le concept racine carrée. On peut facilement
obtenir des phrases comme : ``le nombre positif tel que si on
le multiplie par lui-même on obtient exactement le nombre positif
ni le concept racine carrée. On peut facilement
obtenir des phrases comme : ``le nombre positif tel que si on
le multiplie par lui-même on obtient exactement le nombre positif 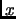 est égal à
est égal à 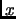 divisé par le nombre positif tel que si l'on le
multiplie par lui-même on obtient exactement le nombre positif
divisé par le nombre positif tel que si l'on le
multiplie par lui-même on obtient exactement le nombre positif 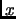 ''.
''.
- Les fonctions
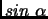 et
et 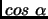 sont définies par
rapport à un cercle de rayon
sont définies par
rapport à un cercle de rayon 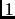 . L'argument
. L'argument 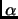 de ces
fonctions est l'angle orienté dans le sens des aiguilles d'une
montre, formé par l'axe des
de ces
fonctions est l'angle orienté dans le sens des aiguilles d'une
montre, formé par l'axe des 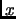 positifs et une demi-droite
passant par l'origine.
La valeur de
positifs et une demi-droite
passant par l'origine.
La valeur de 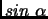 est la coordonnée
est la coordonnée 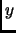 du point d'intersection entre la demi-droite et le cercle tandis que
de
du point d'intersection entre la demi-droite et le cercle tandis que
de 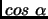 est la coordonnée
est la coordonnée 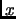 de cette intersection. Afin
d'exprimer une relation comme
de cette intersection. Afin
d'exprimer une relation comme
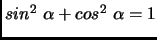 sans
utiliser ni les concepts de sinus et cosinus ni la notation
sans
utiliser ni les concepts de sinus et cosinus ni la notation
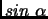 ou
ou 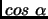 , il faudrait une phrase que sa longueur
rendrait totalement incompréhensible.
, il faudrait une phrase que sa longueur
rendrait totalement incompréhensible.
L'introduction de concepts et de notations est donc à la fois normale
et très souhaitable. Dans le cadre d'un livre, il est important de
choisir avec soin les concepts et notations :
- il faut introduire plusieurs concepts et notations pour des notions
nouvelles pour le lecteur, car le domaine de discours est nouveau
(le graphe),
- en informatique, on introduit souvent un concept ou une notation
pour s'en servir uniquement dans un chapitre d'un livre ou dans un
article scientifique, alors que les concepts et notations mathématiques
sont normalisés depuis longtemps,
- à noter qu'il peut y avoir des variations sur certains concepts et
certaines notations selon l'auteur de l'ouvrage,
- l'informatique manipule des objets plus variés et concrets que la
mathématique. Il faut donc faire plus attention aux
notations utilisées.
Sous-sections




suivant: Concepts et notations ensemblistes
monter: Fondements
précédent: Exercices
Table des matières
Index