Le principe consiste à détecter, à intervalles réguliers, les attentes circulaires, puis de permettre la reprise par une action curative.
debut
tant que vrai faire debut
trouverAttenteCirculaire;
traiterCycle;
attendre delaiPeriode;
fin
fin
traiterCycle utilise généralement une des deux méthodes suivantes :
Soit un système et son graphe d'allocation des ressources,
trouverAttenteCirculaire est facilement implémentable :
debut
tant qu'il existe un sommet sans prédécesseur faire debut
enlever les arcs sortants de ce sommet;
enlever le sommet;
fin
attenteCirculaire = non (graphe résultant est vide)
fin
Il existe des ressources non distinguables (ex : un bloc du disque libre) pour le problème de l'interblocage. Dans ce cas, le graphe des allocations est complexe, et une représentation matricielle est plus aisée et plus efficace.
Un système est composé de ![]() processus et de
processus et de ![]() types de ressources. Le problème de l'interblocage est décrit par : un vecteur
types de ressources. Le problème de l'interblocage est décrit par : un vecteur
![]() des ressources existantes, une matrice
des ressources existantes, une matrice
![]() des ressources tenues, et une matrice
des ressources tenues, et une matrice
![]() des requêtes.
On note
des requêtes.
On note
![]()
trouverAttenteCirculaire(E,T,R) peut alors s'écrire :
debut
![]()
;
tant qu'il existe un processus ![]()
tel que
![]()
faire debut
![]()
;
![]()
;
fin
attenteCirculaire = ![]()
;
fin
![]() représente les ressources disponibles. L'idée intuitive est donc : si le système satisfait la requête
représente les ressources disponibles. L'idée intuitive est donc : si le système satisfait la requête ![]() , alors
, alors ![]() peut terminer son exécution, et rendre ainsi les ressources
peut terminer son exécution, et rendre ainsi les ressources ![]() qu'il détient.
qu'il détient.
Soit un système composé de 3 processus et de 4 types de ressources.
![]() ,
,
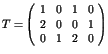 ,
,
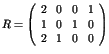 .
.
L'algorithme trouverAttenteCirculaire(E,T,R) donne :
Pour
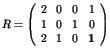 .
.
L'algorithme trouverAttenteCirculaire(E,T,R) donne :
Pour
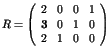 .
.
L'algorithme trouverAttenteCirculaire(E,T,R) donne :
trouverAttenteCirculaire utilise soit un graphe, soit des matrices. Cette information peut être obtenue de deux façons :