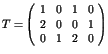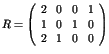Les politiques d'évitement

Pour éviter de devoir choisir entre reprise préemptive et reprise par élimination, il suffit d'éviter les interblocages. Malheureusement, ce n'est pas simple comme le montre l'exemple suivant :

On utilise encore le système composé de 3 processus et de 4 types de ressources.
$E = (5, 2, 3, 1)$, $T = \left( \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 2 & 0 & 0 & 1 \\ 0 & 1 & 2 & 0 \end{array} \right)$, $R = \left( \begin{array}{cccc} 2 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 2 & 1 & 0 & 0 \end{array}\right)$.

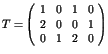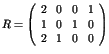L'algorithme trouverAttenteCirculaire nous dit qu'il n'y a pas d'interblocage, et que l'on peut satisfaire aux demandes de $P_3$. Faisons l'hypothèse que $P_3$ ne termine pas aussitôt, mais qu'il souhaite maintenant une ressource de type 4. 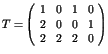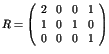La situation est $T = \left( \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 2 & 0 & 0 & 1 \\ 2 & 2 & 2 & 0 \end{array} \right)$, $R = \left( \begin{array}{cccc} 2 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$, qui est une situation d'interblocage car $D = (0, 0, 0, 0)$.

Pour éviter l'interblocage, il ne fallait donc pas donner les ressources à $P_3$, mais c'était la seule évolution possible, c'était donc la requête précédente qui n'aurait pas du être satisfaite...

Plus généralement, toutes les solutions d'évitement doivent connaître l'avenir, et ne sont donc pas implémentable directement. Il existe des algorithmes d'évitement dès que l'on a une connaissance même partielle du futur.

L'algorithme du banquier (Dijkstra)

Nous faisons l'hypothèse qu'au début de son exécution, un processus déclare un vecteur $Max = (m_i,\dots,m_n)$ qui indique, pour chaque type de ressource, le nombre maximum dont il pourra avoir besoin lors de son exécution.

Une situation saine, est une situation dans laquelle même si tous les processus veulent le maximum de ressources, il n'y a pas d'interblocage. A partir d'une telle situation, même dans le pire des cas, on est capable d'ordonner les processus afin que tous terminent.

L'algorithme suivant détermine si une situation est saine ou non.

situationSaine(E,Max,T)
debut
situationSaine = non (trouverAttenteCirculaire(E,T,Max-T));
fin

L'algorithme d'évitement du banquier s'écrit alors :

debut
tant que vrai faire
     pour chaque requête Ri faire
          si situationSaine(E,Max,T+Ri) alors debut
             T = T + Ri;
             Ri = O;
             fin
fin

Supposons qu'au même instant, tous les clients d'une banque décident de retirer tous l'argent qu'ils possèdent sur tous leurs comptes. Si le banquier peut satisfaire ces requêtes, c'est que la situation de la banque est saine. C'est cette analogie qui donne le nom à cet algorithme.

Un exemple

Soit le système décrit par $E = (5, 5, 5, 5)$, $Max = \left( \begin{array}{cccc} 3 & 2 & 3 & 1 \\ 1 & 3 & 2 & 3 \\ 2 & 2 & 2 & 2 \end{array}\right)$ et l'évolution :

$\begin{array}{c\vert c\vert c\vert l} T & R & D & remarques \\ \hline \par\left... ...lgorithme\ du\ banquier\ accepte\ la\ requete\ de\ P1}\\ \hline \par\end{array}$

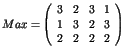Contraintes d'implémentation

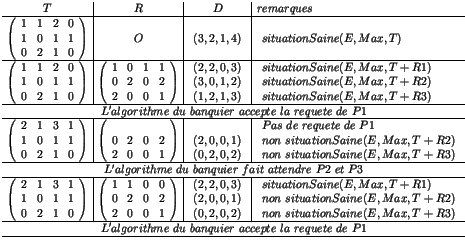
Un algorithme d'évitement ne peut pas travailler à intervalles réguliers, il doit donner son accord pour toutes les requêtes, il doit donc maintenir en permanence ses données. Sa complexité fait qu'il est très coûteux en UC. De plus tous les processus ne sont pas capables de fournir en début d'exécution le vecteur des ressources maximales. L'algorithme du banquier n'est donc pas exploitable dans un système généraliste.