Toute bactérie, indépendamment des autres et indépendamment du passé, peut se diviser en deux avec la probabilité 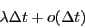 dans l'intervalle de temps
dans l'intervalle de temps 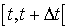 .
.
Les bactéries ne meurent jamais.
A l'instant 0, il y a une seule bactérie dans le tube.
Exercice 1 : Processus de Yule
On considère l'évolution de la population d'une bactérie dans un tube, suivant les conditions suivantes :
Toute bactérie, indépendamment des autres et indépendamment du passé, peut se diviser en deux avec la probabilité 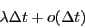 dans l'intervalle de temps
dans l'intervalle de temps 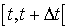 .
.
Les bactéries ne meurent jamais.
A l'instant 0, il y a une seule bactérie dans le tube.
Modéliser le nombre de bactéries à l'instant 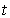 par un processus de naissance pure dont vous donnerez le taux ; dessiner le diagramme de transition.
par un processus de naissance pure dont vous donnerez le taux ; dessiner le diagramme de transition.
Montrer que 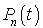 , la probabilité d'avoir une population de
, la probabilité d'avoir une population de 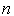 bactéries à l'instant
bactéries à l'instant 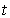 , satisfait le système d'équations différentielles :
, satisfait le système d'équations différentielles :
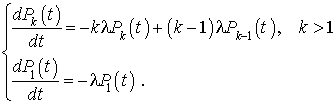
Montrer par une récurrence sur k, qu'on a :
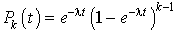
En déduire l'espérance mathématique du nombre de bactéries à l'instant 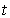 .
.
Considérons maintenant un modèle déterministe, dans lequel chaque bactérie se divise en deux toutes les 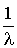 minutes (i.e. le même taux de naissance que dans le modèle probabiliste). En comparant le nombre de bactéries dans le modèle déterministe et le nombre moyen de bactérie dans le modèle probabiliste (tous les deux à l'instant
minutes (i.e. le même taux de naissance que dans le modèle probabiliste). En comparant le nombre de bactéries dans le modèle déterministe et le nombre moyen de bactérie dans le modèle probabiliste (tous les deux à l'instant 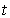 ), que peut-on en déduire ?
), que peut-on en déduire ?
Considérons un atome radioactif (par exemple un atome d'uranium) qui peut se transformer en émettant des particules (ou rayon gamma) en un autre atome. Les différents atomes représentent les états du système, et l'évolution du processus est considérée comme une suite de transitions :
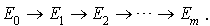
Suivant des théories physiques, la probabilité d'une transition 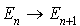 , pendant l'intervalle de temps
, pendant l'intervalle de temps 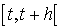 , reste la même aussi longtemps que l'atome reste dans le même état
, reste la même aussi longtemps que l'atome reste dans le même état 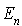 . On pose
. On pose 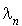 le taux de transition de
le taux de transition de 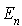 vers
vers 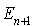 .
.
Modéliser le processus par un processus de mort pure. Dessiner le diagramme de transition. Ecrire le système d'équations différentielles dont la solution donne la probabilité pour que l'atome soit dans l'état 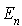 avec
avec 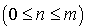 à l'instant
à l'instant 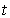 . On ne demande pas de le résoudre.
. On ne demande pas de le résoudre.
Que peut-on dire de la v.a. 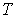 représentant la durée de temps pour que l'atome initial entre dans l'état final
représentant la durée de temps pour que l'atome initial entre dans l'état final 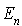 ?
?
Quelle en est l'espérance mathématique ?
 |