Définition
Un processus stochastique 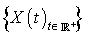 , avec
, avec 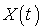 v.a. discrète, est un processus de Markov (ou une chaîne de Markov dans le temps continu), s'il vérifie la propriété sans mémoire :
v.a. discrète, est un processus de Markov (ou une chaîne de Markov dans le temps continu), s'il vérifie la propriété sans mémoire :
Pour toute suite d'instants 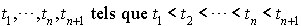 , on a :
, on a :
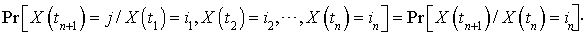
Les processus de Poisson ne connaissent que des incrémentations avec un taux constant. Dans la suite, nous introduirons des processus sans mémoire qui admettent des incrémentations et des décrémentations avec des taux variables, dépendants de l'état actuel du processus. Ces processus, intervenant dans la modélisation de larges classes de phénomènes d'attente, sont appelés processus de naissance et de mort. Ils sont à leur tour des cas particuliers des processus de Markov homogènes dans le temps continu, que nous allons présenter très sommairement ci-dessous.
Définition Un processus stochastique Pour toute suite d'instants |
Cette propriété peut être interprétée par le fait que la probabilité du passage d'un état
Caractérisation des processus de Markov
Dans le cas des chaînes de Markov (temps discret), les transitions ont lieu aux instants
Désignons par E l'ensemble des états du processus de Markov. Soient s et t deux instants, avec
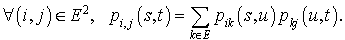
On peut représenter ce système d'équations de façon matricielle :
avec 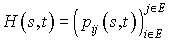 . Cette matrice est appelée matrice de probabilités de transition.
. Cette matrice est appelée matrice de probabilités de transition.
Un processus de Markov est dit homogène, si la matrice de probabilités de transition ne dépend que de
Posons par ailleurs 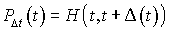 . Lorsque
. Lorsque 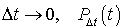 tend vers la matrice unité I. Par conséquent, si l'on souhaite trouver un taux, on doit retrancher la matrice untité I de
tend vers la matrice unité I. Par conséquent, si l'on souhaite trouver un taux, on doit retrancher la matrice untité I de 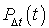 avant de la diviser par
avant de la diviser par 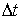 . Posons donc :
. Posons donc :
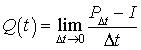
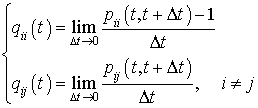
On en déduit, pour 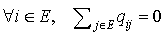 . Pour un processus de Markov donné par son état initial et son générateur infinitésimal, on peut, en principe, trouver la probabilité pour qu'il soit dans un état j à un instant donné t. Toutefois ce calcul est très difficile en pratique et, sauf dans des cas très simples, aucune méthode connue n'aboutit à une expression explicite pour ces probabilités.
. Pour un processus de Markov donné par son état initial et son générateur infinitésimal, on peut, en principe, trouver la probabilité pour qu'il soit dans un état j à un instant donné t. Toutefois ce calcul est très difficile en pratique et, sauf dans des cas très simples, aucune méthode connue n'aboutit à une expression explicite pour ces probabilités.
Si le processus de Markov est homogène, la matrice
Processus de naissance et de mort
Une classe importante de processus de Markov, qui intervient dans l'étude des phénomènes d'attente, est celle des processus de naissance et de mort. Soit 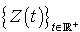 un processus de Markov homogène. Nous identifions les états du processus avec
un processus de Markov homogène. Nous identifions les états du processus avec 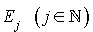 . Le processus
. Le processus 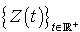 est un processus de naissance et de mort, si les seules transitions directes possibles à partir de
est un processus de naissance et de mort, si les seules transitions directes possibles à partir de 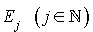 sont :
sont :
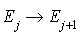 appelée naissance,
appelée naissance,
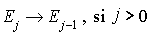 , appelée mort.
, appelée mort.
Un processus de naissance et de mort est de générateur infinitésimal suivant :
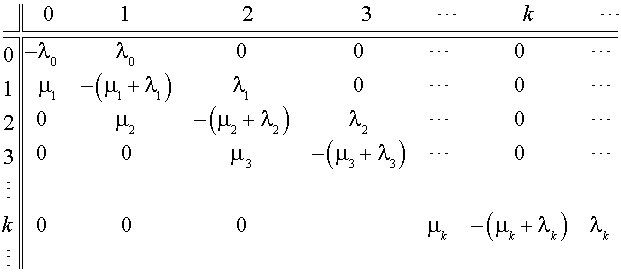
Lorsque le système à un instant donné t est dans l'état
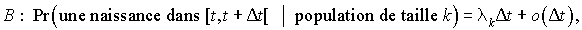
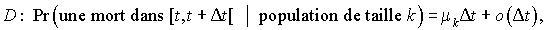
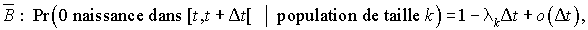
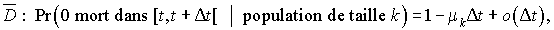
où
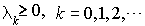 est le taux de naissance pour une population de taille k,
est le taux de naissance pour une population de taille k,
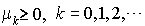 est le taux de mort pour une population de taille k
est le taux de mort pour une population de taille k 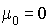 )
)
Plus intuitivement, on peut énoncer la propriété caractéristique suivante :
Supposons que l'on observe l'évolution d'un processus de naissance et de mort de taille k à l'instant t, en considérant un intervalle de temps de durée 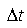 , avec
, avec 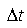 assez petit. Alors, pendant l'intervalle
assez petit. Alors, pendant l'intervalle 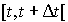 , il peut survenir une naissance avec une probabilité proportionnelle à
, il peut survenir une naissance avec une probabilité proportionnelle à 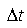 ou une mort avec une probabilité proportionnelle à
ou une mort avec une probabilité proportionnelle à 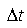 , les coefficients de proportionnalité étant respectivement de
, les coefficients de proportionnalité étant respectivement de 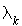 et de
et de 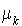 (dépendants donc de la taille).
(dépendants donc de la taille).
Notons que ces probabilités ne sont pas affectées quelque soit l'instant t (propriété d'homogénéité) et quelques fussent les événements qui ont mené le processus dans son état actuel (propriété sans mémoire).
Soit 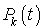 la probabilité pour que la population soit de taille k à l'instant t :
la probabilité pour que la population soit de taille k à l'instant t :
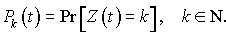
Dans un premier temps, nous cherchons à déterminer 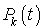 .
.
Proposition 6 Soit |
Démonstration. Considérons deux
instants t et 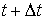 et calculons la probabilité pour que le processus soit de taille k (état
et calculons la probabilité pour que le processus soit de taille k (état 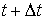 en fonction de son état à l'instant t.
en fonction de son état à l'instant t.
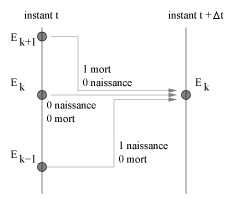
Passage de l'état de l'instant t à l'instant 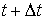
Nous avons pour
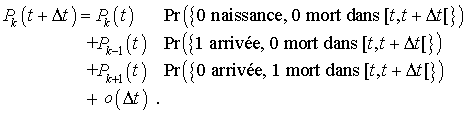
Les probabilités associées aux événements 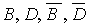 , permettent d'écrire :
, permettent d'écrire :
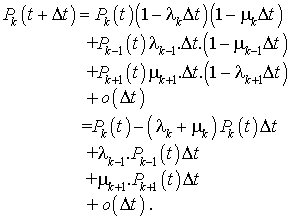
En regroupant les termes et en divisant les membres par 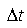 , il vient :
, il vient :
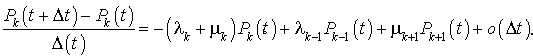
Sachant que 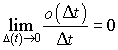 , on obtient :
, on obtient :
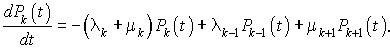
Cette relation, pour 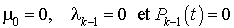 . Par ailleurs, la somme des probabilités vaut 1 et, donc,
. Par ailleurs, la somme des probabilités vaut 1 et, donc, 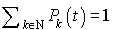 . D'où la proposition.
. D'où la proposition.
On peut donner une version matricielle pour cette proposition, qui ressemble à l'équation matricielle pour les chaînes de Markov.
Désignons par deux vecteurs lignes
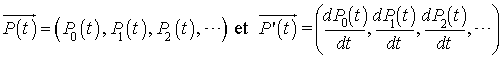
constitués respectivement des probabilités et de leurs dérivées. Le système d'équations différentielles de la proposition 1 s'écrit alors :
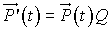
où Q est le générateur infinitésimal du processus de naissance et de mort.
Diagramme de transition et interprétation intuitive
On associe à un processus de naissance et de mort un graphe fini ou infini (suivant la finitude ou l'infinitude du processus), valué de la façon suivante :
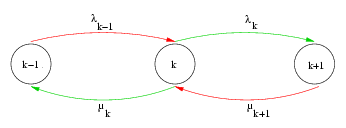
Taux de flux de probabilité entrant en 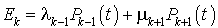 .
.
Taux de flux de probabilité sortant en 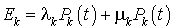 .
.
On en déduit le taux de variation de probabilité :
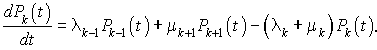
Devant une cabine téléphonique, les usagers arrivent un par un pour téléphoner. Si elle est libre, le premier occupe la cabine, sinon il s'en va définitivement.
On suppose que, dans l'intervalle de temps 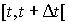 la probabilité pour qu'un usager arrive est
la probabilité pour qu'un usager arrive est 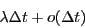 et que, dans le même intervalle de temps, la probabilité pour qu'une conversation téléphonique engagée prenne fin est
et que, dans le même intervalle de temps, la probabilité pour qu'une conversation téléphonique engagée prenne fin est 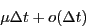 ; et ceci indépendamment des événements qui précèdent l'instant t.
; et ceci indépendamment des événements qui précèdent l'instant t.
Le système est modélisé par un processus de naissance et de mort à deux états : libre 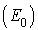 et occupé
et occupé 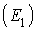 . On a :
. On a :
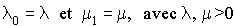 .
.
Rappelons en effet que 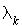 est le taux de naissance pour une population de taille k et vaut 0 pour
est le taux de naissance pour une population de taille k et vaut 0 pour 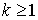 dans cet exemple. De même,
dans cet exemple. De même, 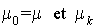 n'existe pas pour
n'existe pas pour
Par conséquent, le processus admet le diagramme de transition suivant :
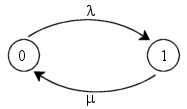
Les équations de la proposition 6 deviennent :
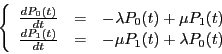
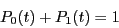
Portons la valeur  dans la première équation ; il vient :
dans la première équation ; il vient : 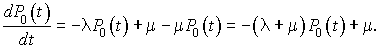
C'est une équation différentielle linéaire avec second membre. La solution de l'équation sans second membre associée est 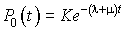 . On pose donc
. On pose donc 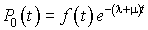 .
.
Portant cette valeur dans l'équation avec second membre, après les simplifications nécessaires, on aura : 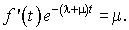 Donc :
Donc : 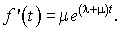
On en déduit : 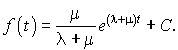
Nous aurons finalement :
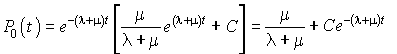 .
.
Si l'on impose la condition initiale que la cabine est libre à l'instant 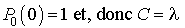 .
.
Nous aurons alors des expressions explicites et simples pour la probabilité pour que la cabine soit libre et la probabilité pour qu'elle soit occupée. On a :
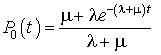
et
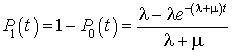 .
.
Si 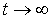 , nous aurons :
, nous aurons :
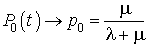
et
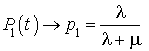 .
.