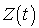 le nombre de bactéries dans le tube à l'instant
le nombre de bactéries dans le tube à l'instant 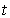 . Il est clair que
. Il est clair que 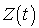 est une instance particulière des processus de naissance pure de taux variable.
est une instance particulière des processus de naissance pure de taux variable.Solution de l'exercice 1 : Processus de Yule
a. Désignons par 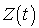 le nombre de bactéries dans le tube à l'instant
le nombre de bactéries dans le tube à l'instant 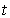 . Il est clair que
. Il est clair que 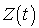 est une instance particulière des processus de naissance pure de taux variable.
est une instance particulière des processus de naissance pure de taux variable.
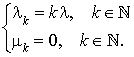
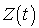 a le diagramme de transition suivant :
a le diagramme de transition suivant :
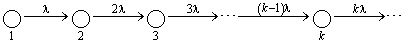
b. En portant 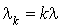 et
et 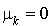 dans le système d'équations qui régit les processus de naissance et de mort nous aurons :
dans le système d'équations qui régit les processus de naissance et de mort nous aurons :
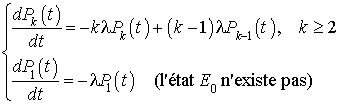
La condition initiale est  .
.
c. Pour  , nous avons :
, nous avons :
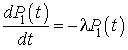
Cette équation admet la solution générale 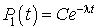 . Tenant compte de la condition initiale, nous aurons
. Tenant compte de la condition initiale, nous aurons 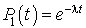 . Donc pour
. Donc pour  , nous avons bien
, nous avons bien
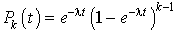 . Supposons l'égalité vraie pour
. Supposons l'égalité vraie pour  et montrons-la pour
et montrons-la pour 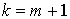 .
.
Nous avons l'équation différentielle : 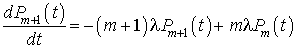 .
.
Sachant que 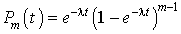 , il vient alors :
, il vient alors :  .
.
La méthode de résolution utilisée pour les processus de Poisson s'applique et nous obtenons la solution associée à l'équation  pour obtenir l'expression
pour obtenir l'expression  .
.
Posons alors  et portons
et portons  dans l'équation différentielle initiale. Après les simplifications nécessaires il vient :
dans l'équation différentielle initiale. Après les simplifications nécessaires il vient :
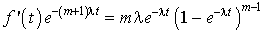 .
.
D'où 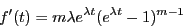 . Donc
. Donc 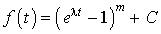 .
.
On en déduit 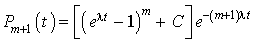 .
.
La condition initiale  implique
implique  et donc
et donc
 .
.
Ce qui prouve que  est la forme proposée.
est la forme proposée.
d. L'espérance mathématique du nombre de bactéries à l'instant 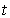 est donnée par :
est donnée par :
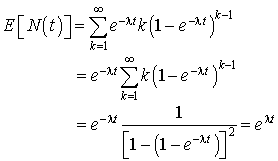
e. Dans le modèle déterministe, à l'instant 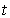 , le nombre de bactéries vaut :
, le nombre de bactéries vaut :
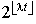 où
où  désigne la partie entière de
désigne la partie entière de  .
.
Puisque  , on en déduit que pour le même taux de naissance, le nombre moyen de bactéries dans le modèle probabiliste est beaucoup plus élevé que le même nombre dans me modèle déterministe !
, on en déduit que pour le même taux de naissance, le nombre moyen de bactéries dans le modèle probabiliste est beaucoup plus élevé que le même nombre dans me modèle déterministe !
 |