Proposition 2.
Si 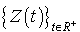 est un processus de Poisson de taux
est un processus de Poisson de taux 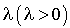 , alors la variable aléatoire T suit une loi exponentielle de paramètre
, alors la variable aléatoire T suit une loi exponentielle de paramètre 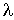 . On a donc :
. On a donc :
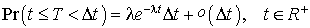
Soit
Proposition 2. Si
|
Démonstration.
Soit 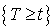 correspond à
correspond à
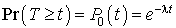
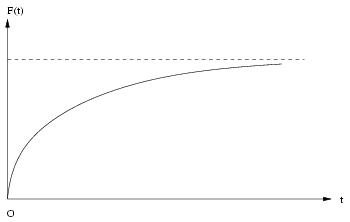
Donc la fonction de répartition de
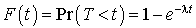
Par conséquent, la v.a.
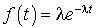
La réciproque est également vraie.
Proposition 3. Si les interarrivées forment des v.a. indépendantes (dans leur ensemble), chacune suivant une loi exponentielle de paramètre |
Démonstration.
A l'instant 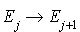 . Considérons par ailleurs un intervalle de temps
. Considérons par ailleurs un intervalle de temps 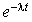 . Mais cette expression se développe en
. Mais cette expression se développe en 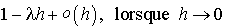 . On en déduit que la probabilité d'une arrivée dans l'intervalle est
. On en déduit que la probabilité d'une arrivée dans l'intervalle est 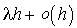 .
.
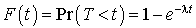
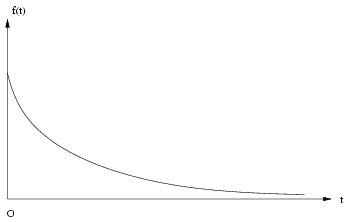
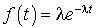
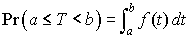
Rappelons sans preuve les résultats suivants, qui font partie des propriétés simples des v.a. exponentielles, voir [4].
Proposition 4. On considère un processus de Poisson de taux
|
La propriété ci-dessous est une particularité caractéristique de la loi exponentielle.
Proposition 5. La loi exponentielle est une loi « sans mémoire » :
|
Démonstration.
Nous avons :
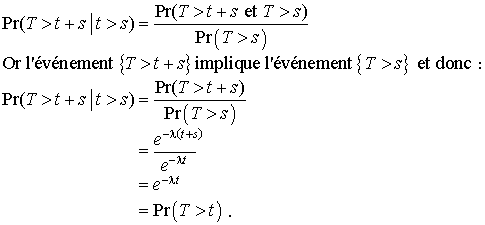
On peut aussi démontrer la réciproque. C'est-à-dire si 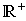 , alors
, alors
Application des processus de Poisson et de la loi exponentielle
Les processus de Poisson peuvent modéliser de nombreux phénomènes réels. Des tests statistiques, fondés sur des observations, permettront de juger si l'on peut raisonnablement faire appel à ce modèle dans des circonstances données. Bien que ces vérifications sortent du cadre de l'objectif que nous nous sommes donné ici, vue l'importance pratique, nous en traiterons quelques exemples simples dans une séquence ultérieure.Faisons dès maintenant les remarques suivantes.
Considérons les occurrences aléatoires aléatoires d'un événement qui se réalisent de façon homogène dans le temps continu et sans liens causaux. A titre d'exemples on peut inclure les cas :
de désintégrations d'une particule radioactive,
d'arrivées d'usagers dans un établissement,
de défaillances survenues dans un ensemble d'un grand nombre d'un même équipement, qui ne connait pas l'usure.
Si 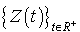 . Ce processus pourra donc être assimilé à un processus de Poisson et la durée de temps, qui sépare deux occurrences consécutives sera une v.a. qui suit une loi exponentielle.
. Ce processus pourra donc être assimilé à un processus de Poisson et la durée de temps, qui sépare deux occurrences consécutives sera une v.a. qui suit une loi exponentielle.
De même, lorsqu'on étudie la durée de vie d'un équipement sans usure (ou une particule peu stable) dans le temps supposé homogène, on pourra postuler que la propriété sans mémoire est satisfaite pour cette durée et, donc, qu'elle suit une loi exponentielle d'un paramètre, qui reste à déterminer.
Questionnaire de compréhension immédiate