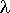 , pour l'entier positif
, pour l'entier positif 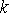 fixé,
fixé, 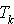 désigne la durée de temps qui sépare
désigne la durée de temps qui sépare 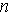 et
et  arrivées. C'est une v.a. à valeurs dans
arrivées. C'est une v.a. à valeurs dans 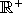 . Elle généralise le concept d'interarrivée que nous avons étudiée. On a en effet
. Elle généralise le concept d'interarrivée que nous avons étudiée. On a en effet 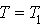 .
.Etant donné un processus de Poisson de taux 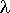 , pour l'entier positif
, pour l'entier positif 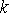 fixé,
fixé, 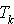 désigne la durée de temps qui sépare
désigne la durée de temps qui sépare 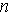 et
et  arrivées. C'est une v.a. à valeurs dans
arrivées. C'est une v.a. à valeurs dans 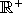 . Elle généralise le concept d'interarrivée que nous avons étudiée. On a en effet
. Elle généralise le concept d'interarrivée que nous avons étudiée. On a en effet 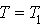 .
.
Montrer que la fonction de répartition de 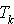 est donnée par :
est donnée par :
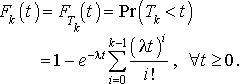
En déduire la densité de 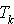 :
:

C'est la densité de la loi Gamma de paramètres 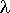 et
et 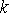 . On rappelle la définition de l'intégrale eulérienne :
. On rappelle la définition de l'intégrale eulérienne :
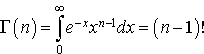
Calculer l'espérance mathématique et la variance de 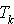 , en utilisant l'intégrale eulérienne.
, en utilisant l'intégrale eulérienne.
Peut-on calculer les paramètres précédents sans passer par des intégrales eulériennes ?
 |