Exercices

Définition 9.4   Une boucle est une arête dont les deux extrémités sont identiques.

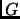
Exercice 9.1   Pour le type abstrait centré-sommets, écrire un algorithme qui compte le nombre de boucles dans un graphe $G$ donné.

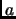
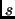
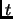
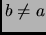
Définition 9.5   Une arête multiple est une arête $a$ d'extrémités $s$ et $t$, telle qu'il existe une arête $b \neq a$ avec les mêmes extrémités.

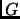
Exercice 9.2   Pour le type abstrait centré-sommets, écrire un algorithme qui compte le nombre d'arêtes multiples dans un graphe $G$ donné.

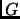
Exercice 9.3   Pour le type abstrait centré-arêtes, écrire un algorithme qui compte le nombre d'arêtes multiples dans un graphe $G$ donné.

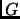
Définition 9.6   Un cycle Hamiltonien dans un graphe $G$ est un cycle
$C = s_1, e_1, s_2, e_2, \ldots, s_n, e_n, s_1$,
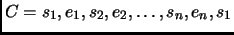
tel que
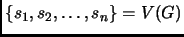
$\{s_1, s_2, \ldots, s_n\} = V(G)$ et $\forall i, j \in [1, n], s_i = s_j \Rightarrow i = j$.

Autrement dit, le cycle doit contenir tout les sommets du graphe, et chaque sommet doit figurer exactement une fois. Par contre, il n'y a pas d'obligation pour chaque arête d'y figurer.

Exercice 9.4   Prouver qu'une boucle (voir définition 9.4) ne peut pas figurer dans un cycle Hamiltonien.

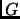
Exercice 9.5   Écrire un algorithme qui cherche une cycle Hamiltonien dans un graphe $G$ quelconque.

Définition 9.7   Un arbre non orienté est un graphe non orienté ne contenant pas de cycle.

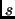
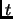
Exercice 9.6   Prouver que dans un arbre non orienté, entre deux sommets quelconques $s$ et $t$, il existe au plus une chaîne.

Exercice 9.7   Simplifier l'algorithme 9.6 dans le cas où l'on sait que le graphe d'entrée est un arbre non orienté.