Entrée : Un graphe
Sortie : Une valeur booléenne indiquant si le nombre de sommets de degré impair est soit zéro soit deux. Algorithme :
- initialiser un accumulateur
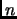 à
à 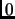 ,
,
- utiliser l'opération NB_NODES(G) pour récupérer le
nombre de sommets,
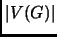 , de
, de 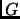 ,
,
- pour
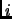 allant de
allant de 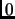 à
à 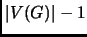 faire :
faire :
- utiliser l'opération NODE(G, i) pour récupérer
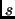 le
sommet numéroté
le
sommet numéroté 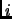 de
de 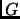 .
.
- utiliser l'opération NB_EDGES(s) pour déterminer le
degré
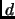 de
de 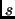 ,
,
- si
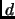 et impair, alors incrémenter (additionner
et impair, alors incrémenter (additionner 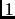 à)
à) 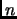 ,
,
- utiliser l'opération NODE(G, i) pour récupérer
- si
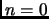 ou
ou 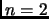 alors renvoyer ``oui'', sinon renvoyer ``non''
alors renvoyer ``oui'', sinon renvoyer ``non''