La programmation linéaire est un cas simple mais important du problème général d'optimisation mathématique de trouver la valeur optimale (maximum ou minimum selon le cas) d'une fonction mathématique étant donné un nombre de restrictions (contraintes) sur les valeurs des paramètres. En général, les problèmes de ce type peuvent être très compliqués à résoudre mais dans le cas de la programmation linéaire des algorithmes efficaces sont connus mais un nombre énorme de problèmes réels et importants peuvent être exprimés par des programmes linéaires.
Définition: un programme linéaire sur ![]() variables
(par convention nous écrivons les variables
variables
(par convention nous écrivons les variables
![]() )
est d'optimiser (minimiser ou maximiser) une fonction
linéaire dans les variables étant donné des contraintes linéaires dans les variables.
)
est d'optimiser (minimiser ou maximiser) une fonction
linéaire dans les variables étant donné des contraintes linéaires dans les variables.
[Une fonction linéaire est une fonction qui peut être exprimée
comme
![]() ; on ignore le
; on ignore le ![]() de la fonction à optimiser
(la fonction objective ou économique) parce qu'elle
ne change en rien la question. Une contrainte linéaire
est qu'une fonction linéaire doit être supérieure
ou égale à une autre; par une simple manipulation
algébrique on peut toujours supposer que la première a le
terme constante 0 et la deuxième
est une fonction triviale constante
On obtient donc une condition de la forme de:
de la fonction à optimiser
(la fonction objective ou économique) parce qu'elle
ne change en rien la question. Une contrainte linéaire
est qu'une fonction linéaire doit être supérieure
ou égale à une autre; par une simple manipulation
algébrique on peut toujours supposer que la première a le
terme constante 0 et la deuxième
est une fonction triviale constante
On obtient donc une condition de la forme de:
![]() .]
.]
Une usine de verre peut produire de la verre de qualité basse, moyenne ou supérieure; une tonne de la basse qualité nécessite 3 tonnes de sables, 500gms d'additifs et 1 heure du travail d'un ouvrier; pour les deux autres qualités, les chiffres correspondants sont (moyenne) 3.2 tonnes, 1000gms et 1,5 heures; (supérieure) 3.5 tonnes, 2500 gms et 4 heures. Les bénéfices de la vente d'une tonne sont de 100, 200 et 300 Euros. Chaque semaine 200 tonnes de sable et 120000 gms d'additif sont disponibles et il y a 6 ouvriers chacun travaillant au maximum 35 heures/semaine. Quelles quantités doit-on produire chaque semaine pour maximiser les bénéfices?
On écrit
![]() pour les quantités produites de chaque
qualité.
pour les quantités produites de chaque
qualité.
On veut maximiser
![]() avec les contraintes:
avec les contraintes:
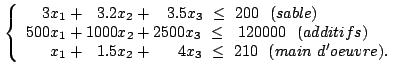
Un programme linéaire en forme canonique est à maximiser
une fonction
![]() avec
avec ![]() contraintes
dont la i-ème est:
contraintes
dont la i-ème est:
![]() et aussi les contraintes implicites que chaque
et aussi les contraintes implicites que chaque
![]() .
.
Il est claire que tout programme linéaire peut être
transformé en un programme équivalent en forme canonique;
un tel programme est résumé par la matrice ![]() des
des ![]() et les deux vecteurs
et les deux vecteurs ![]() et
et ![]() .
.
On appelle solution du programme n'importe quel
vecteur de valeurs ![]() ; les solutions qui respectent toutes les contraintes
sont les solutions réalisables;
un programme qui admet au moins une solution réalisable
est un programme faisable. Pour un programme faisable,
on appelle solution optimale une solution réalisable
où la fonction objective prend sa valeur maximale parmi
toutes les solutions réalisables.
(On dit aussi de façon inexacte que cette valeur maximale
est la ``solution optimale''.)
; les solutions qui respectent toutes les contraintes
sont les solutions réalisables;
un programme qui admet au moins une solution réalisable
est un programme faisable. Pour un programme faisable,
on appelle solution optimale une solution réalisable
où la fonction objective prend sa valeur maximale parmi
toutes les solutions réalisables.
(On dit aussi de façon inexacte que cette valeur maximale
est la ``solution optimale''.)
Il y a des cas où la recherche de ``la solution optimale'' ne peut pas réussir; il est important de savoir quels sont ces cas parce qu'un programme doit pouvoir les traiter:
le programme n'est pas faisable; impossible de trouver la meilleure solution réalisable s'il n'y en a pas;
il existe plusieurs solutions optimales; laquelle sera considérée ``la solution optimale''?
solution infinie: si la fonction économique peut prendre des valeurs indéfiniment grandes parmi les solutions réalisables, il n'est pas question de trouver une solution optimale parce qu'il n'y pas de valeur maximale de la fonction.
le programme n'est pas faisable:
![]()
il existe plusieurs solutions optimales:
![]() , maximiser
, maximiser ![]()
solution infinie:
![]() , maximiser
, maximiser ![]()
(pour tout nombre positif ![]() ,
, ![]() est une solution réalisable
avec valeur
est une solution réalisable
avec valeur ![]() de la fonction économique.)
de la fonction économique.)