Les problèmes suivants, sont-ils des programmes linéaires? (dans tous les exercices sauf si explicité, les contraintes implicites que toutes les variables sont positives ou nulles sont valables.)
- Minimiser
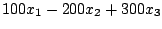 avec les contraintes :
avec les contraintes :
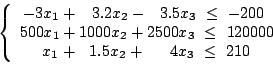
- Maximiser
 avec les contraintes :
avec les contraintes :

- Minimiser
 avec les contraintes :
avec les contraintes :

- Maximiser
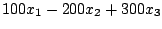 avec les contraintes :
avec les contraintes :

- Maximiser
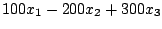 avec les contraintes :
avec les contraintes :
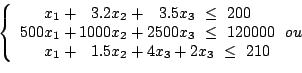
Lesquelles des solutions suivantes du programme de l'usine de verre sont réalisables?

 Consulter la solution...
Consulter la solution...