
Dans les séquences précédentes, nous avons introduit et étudié des modèles mathématiques simples permettant de prédire l'évolution probabiliste d'un système complexe dans le temps, le but étant de prendre une décision convenable chaque fois qu'un choix s'imposait. L'élaboration d'un modèle mathématique adéquat nécessite une étude approfondie, pour fournir des résultats analytiques très précis sur l'évolution du système.
Malheureusement, une résolution mathématique complète reste souvent hors de portée et les méthodes connues ne fournissent que dans des cas très simples une caractérisation explicite de la distribution de probabilité dans le temps. A titre d'exemple, un problème difficile à résoudre est la résolution d'un système d'équations différentielles. Sauf dans des cas très simples, nous nous sommes abstenus de donner une méthode pour sa résolution et nous nous sommes limités à l'étude de la distribution stationnaire. Or une étude de la transition de la distribution initiale vers celle-ci apparaît souhaitable dans beaucoup de circonstances.
Les méthodes numériques peuvent fournir des approximations des solutions recherchées. Ces approches peuvent aboutir à un calcul approximatif des paramètres intéressants du modèle. Toutefois elles souffrent de plusieurs difficultés intrinsèques. Les résultats numériques sont difficiles à interpréter face au poids d'erreurs dont l'importance est souvent méconnue. De plus, les calculs sont souvent complexes et il existe des modèles mathématiques pour lesquels les algorithmes mathématiques connus restent inefficaces.
Une autre approche calculatoire est la simulation. Cette technique abandonne entièrement toute analyse mathématique et se limite à une « imitation » du système étudié. Ce dispositif est appelé modèle de simulation. Dans d'innombrables circonstances un modèle de simulation est conceptuellement très simple et peut fournir des informations quantitatives là où les méthodes mathématiques échouent.
Il faut également noter que la technique de simulation ne se limite pas à l'étude de systèmes d'attente mais s'applique aux phénomènes inadaptés aux études analytiques, qu'il s'agisse de phénomènes déterministes ou aléatoires. Néanmoins, la modélisation des systèmes d'attente fournit un prototype d'application de la technique.
La simulation souffre, à son tour, de plusieurs inconvénients. En particulier, elle produit un volume important de résultats qui nécessitent d'être résumés pour une interprétation. Ceux-ci, contrairement à des propriétés déduites d'une étude analytique, qui sont d'une certaine façon universelles, sont étroitement applicables au système modélisé. Ces résultats sont de nature statistique et peuvent donc être interprétés de manière équivoque. En dépit de ces inconvénients, la simulation reste un outil privilégié dans l'étude des comportements des systèmes complexes et les prédictions qui en sont issues jouissent d'un haut degré de confiance aussi bien chez les scientifiques que chez les industriels.
Exemple 1.a : simulation d'événements suivants
Dans un système à simuler, des événements arrivent dans le temps suivant un mécanisme établi. L'idée fondamentale d'un modèle simulateur est de construire une histoire détaillée des événements. Cette histoire est appelée liste d'événements. Une analyse statistique est alors effectuée pour évaluer les paramètres du système.
Exemple : (Ecker, Kupferschmidt)
Considérons un système d'attente à un seul serveur et supposons que les interarrivées soient des variables aléatoires indépendantes et uniformément distribuées entre 1 et 5 mn. La durée de service est supposée être une v.a. uniformément distribuée entre 2 et 3 mn. Les usagers arrivant à des instants aléatoires, suivant le processus indiqué, sont servis lorsque le serveur est libre puis, s'en vont. Un observateur peut noter les temps d'arrivée, de début de service et de fin de service pour chaque usager au cours d'une journée. On peut ensuite calculer la moyenne des durées d'attente, la longueur moyenne de la file ainsi que d'autres paramètres du système. Ces valeurs ne décriront certes que le jour d'observation mais elles seront probablement une bonne estimation des comportements moyens pendant une longue durée de temps.
Une simulation imite donc le comportement d'un système, réel ou hypothétique, de sorte que les observations puissent se faire sans la réalisation physique du système et sans perte de temps pour collecter les observations.
Construction d'une liste d'événements simulés
Pour montrer la construction typique d'une suite d'événements, considérons le système précédent et supposons que la première arrivée ait lieu à l'instant 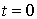 et qu'à cet instant il n'y ait pas d'autres usagers dans le système. Cet usager est immédiatement servi et la fin de service se situe entre
et qu'à cet instant il n'y ait pas d'autres usagers dans le système. Cet usager est immédiatement servi et la fin de service se situe entre 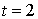 et
et 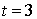 . La deuxième arrivée a lieu entre les instants
. La deuxième arrivée a lieu entre les instants 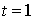 et
et 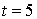 . La simulation ne peut être justifiée que si l'on admet l'hypothèse fondamentale suivante :
. La simulation ne peut être justifiée que si l'on admet l'hypothèse fondamentale suivante :
Les propriétés statistiques à long terme du système réel restent identiques à celles de la suite hypothétique d'événements construits, en tirant au hasard leurs temps d'occurrence respectifs suivant les distributions données initialement. |
Suivant cette hypothèse, nous pouvons construire une suite typique d'événements en choisissant les temps respectifs d'occurrences. Sur l'exemple étudié, il suffit de tirer au hasard uniformément les interarrivées dans l'intervalle 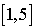 et les durées de service dans
et les durées de service dans 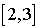 . Si nous supposons que le tirage aléatoire pour l'interarrivée est 3,9 et le tirage pour la durée de service 2,2 mn, alors la liste d'observation sera :
. Si nous supposons que le tirage aléatoire pour l'interarrivée est 3,9 et le tirage pour la durée de service 2,2 mn, alors la liste d'observation sera :
Temps t |
événements |
|
L'usager 1 arrive, il est servi. |
2,2 |
L'usager 1 part, le serveur est libre. |
3,9 |
L'usager 2 arrive, il est servi. |
La flèche pointe sur le temps simulé et montre tous les événements qui peuvent être programmés une fois que l'événement indiqué par ce temps et tous les événements précédents ont eu lieu.
L'événement suivant : départ de l'usager 1, aura lieu à l'instant 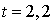 . On n'a donc pas besoin de considérer t dans
. On n'a donc pas besoin de considérer t dans 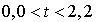 ; c'est pourquoi l'approche est appelée simulation d'événements suivants.
; c'est pourquoi l'approche est appelée simulation d'événements suivants.
Maintenant nous pouvons avancer l'heure de simulation à l'événement suivant, ayant lieu à l'instant 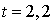 . Cet événement ne permet pas de programmer des événements futurs car aucun usager n'est en attente de service, il ne se passe rien jusqu'à l'arrivée du deuxième usager.
. Cet événement ne permet pas de programmer des événements futurs car aucun usager n'est en attente de service, il ne se passe rien jusqu'à l'arrivée du deuxième usager.
Avançons maintenant le temps simulé à 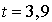 : l'usager 2 arrive.
: l'usager 2 arrive.
Il est maintenant possible de programmer l'arrivée suivante en tirant au hasard une interarrivée dans 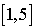 . Si nous tirons 1,7 l'arrivée de l'usager 3 aura lieu à l'instant
. Si nous tirons 1,7 l'arrivée de l'usager 3 aura lieu à l'instant 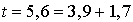 .
.
Dès l'arrivée de cet usager il est possible de programmer son départ en tirant une durée de service dans 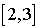 . Si le tirage donne 2,9 alors son départ est programmé à l'instant
. Si le tirage donne 2,9 alors son départ est programmé à l'instant 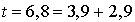 , la suite d'événement est maintenant :
, la suite d'événement est maintenant :
Temps t |
événements |
0,0 |
L'usager 1 arrive, il est servi. |
2,2 |
L'usager 1 part, le serveur est libre. |
|
L'usager 2 arrive, il est servi. |
5,6 |
L'usager 3 arrive, il attend. |
6,8 |
L'usager 2 part. |
6,8 |
L'usager 3 est servi. |
Notons que l'arrivée de l'usager 3 avant le départ de l'usager 2 entraîne une attente de 0,8 mn. Donc, l'arrivée de l'usager 3 à l'instant 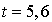 ne permet pas de programmer son départ. Elle permet toutefois de programmer l'arrivée de l'usager 4. Si le tirage donne l'instant
ne permet pas de programmer son départ. Elle permet toutefois de programmer l'arrivée de l'usager 4. Si le tirage donne l'instant 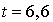 la liste devient :
la liste devient :
Temps t |
événements |
0,0 |
L'usager 1 arrive, il est servi. |
2,2 |
L'usager 1 part, le serveur est libre. |
3,9 |
L'usager 2 arrive, il est servi. |
|
L'usager 3 arrive, il attend. |
6,6 |
L'usager 4 arrive, il attend. |
6,8 |
L'usager 2 part. |
6,8 |
L'usager 3 est servi. |
En avançant le temps simulé à l'événement suivant, nous faisons arriver l'usager 5. Si le tirage donne 1,8 il arrivera à l'instant 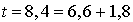 . On a alors :
. On a alors :
Temps t |
événements |
0,0 |
L'usager 1 arrive, il est servi. |
2,2 |
L'usager 1 part, le serveur est libre. |
3,9 |
L'usager 2 arrive, il est servi. |
5,6 |
L'usager 3 arrive, il attend. |
|
L'usager 4 arrive, il attend. |
6,8 |
L'usager 2 part. |
6,8 |
L'usager 3 est servi. |
8,4 |
L'usager 5 arrive |
A ce stade nous ne savons pas si l'usager 5 attend. En effet le départ des usagers 3 et 4 n'est pas programmé. Le départ de l'usager 2 à l'instant 6,8 permet de programmer le départ de l'usager 3 à l'instant 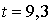 (on a tiré 2,5).
(on a tiré 2,5).
Temps t |
événements |
0,0 |
L'usager 1 arrive, il est servi. |
2,2 |
L'usager 1 part, le serveur est libre. |
3,9 |
L'usager 2 arrive, il est servi. |
5,6 |
L'usager 3 arrive, il attend |
6,6 |
L'usager 4 arrive, il attend. |
6,8 |
L'usager 2 part. |
|
L'usager 3 est servi. |
8,4 |
L'usager 5 arrive. |
9,3 |
L'usager 3 part. |
9,3 |
L'usager 4 est servi. |
Nous pouvons maintenant dire que l'usager 5 va trouver le serveur occupé et doit attendre. Certes, au moment de la construction de la liste, il n'est pas utile de prévoir et noter si un usager va attendre ou non. Ces événements sont les conséquences des arrivées et des durées de service, ils peuvent être rajoutés quand la liste est complète. Nous les avons inclus pour aider le lecteur.
Il est possible de dresser un schéma général du processus générateur d'événements.
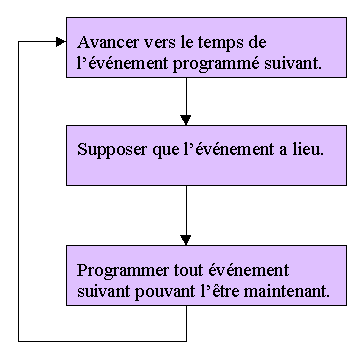
Le processus de programmation d'événements suivants avance le temps simulé à l'événement programmé suivant, autorisant l'occurrence de cet événement, programmant les événements à venir. Ce processus continue jusqu'à produire une histoire de longueur souhaitée.
| |
Le lecteur pourra réaliser lui-même cette simulation à l'aide d'un tableur. Une telle simulation lui est proposée ici au travers d'une feuille EXCEL. |
| Microsoft Excel - 26,0Ko | |
 |
Aide : description de la feuille EXCEL présentée ci-dessus. |
Besoin d'une visionneuse Excel ? Vous pouvez la télécharger à cette adresse. Les utilisateurs de Mac OS préfèreront cette page de téléchargement. Enfin, Sun OpenOffice peut constituer une solution alternative pour de nombreux OS, en particulier Linux.
Exemple 1.b : analyse statistique des résultats de simulation
Une liste d'événements peut être utilisée, de la même façon qu'une liste d'observations, pour estimer diverses propriétés statistiques du système étudié.
Estimation de 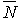 et de
et de 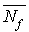
Pour l'exemple précédent, nous avons la courbe de variation de 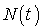 .
.
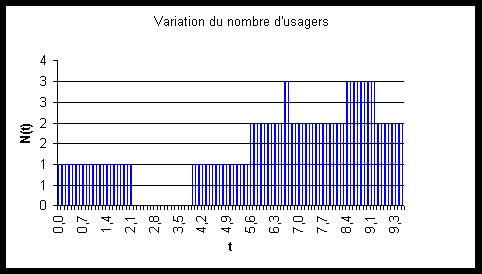
Le nombre moyen d'usagers dans le système vaut : 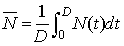 ,
,
où D est la durée de simulation, et N(t) le nombre d'usagers à l'instant t. En utilisant la courbe de variation d'usagers il vient :
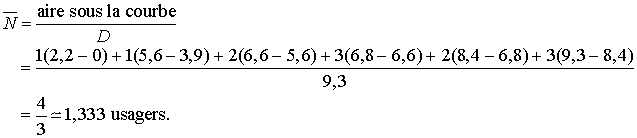 avec un calcul similaire pour la longueur de file d'attente, nous aurons :
avec un calcul similaire pour la longueur de file d'attente, nous aurons :
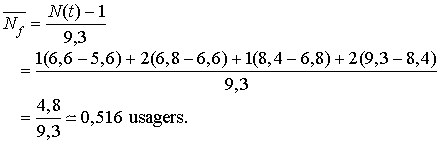
Estimation de 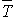 et de
et de 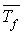
Pour estimer le temps moyen d'attente passé par usager dans le système, nous calculons ce temps pour chaque usager et en déduisons la valeur moyenne.
Usagers |
||
1 |
|
|
2 |
|
|
3 |
|
|
4 |
? |
|
5 |
? |
Notons qu'à l'instant 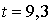 l'usager 4 vient d'être servi et l'usager 5 est en attente et, donc, leur temps passés dans le système ne peuvent être déterminés que si la simulation continue. Dans le modèle de simulation il arrive souvent que des tâches n'arrivent pas à l'aboutissement prévu et, dans ce cas, les travaux non terminés ne sont pas comptabilisés dans les statistiques.
l'usager 4 vient d'être servi et l'usager 5 est en attente et, donc, leur temps passés dans le système ne peuvent être déterminés que si la simulation continue. Dans le modèle de simulation il arrive souvent que des tâches n'arrivent pas à l'aboutissement prévu et, dans ce cas, les travaux non terminés ne sont pas comptabilisés dans les statistiques.
Le temps moyen passé dans la file d'attente se calcule de façon similaire.
Usagers |
||
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
? |
Facteur d'utilisation
On peut estimer 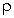 à partir de la suite d'événements :
à partir de la suite d'événements :
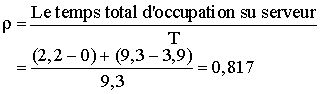
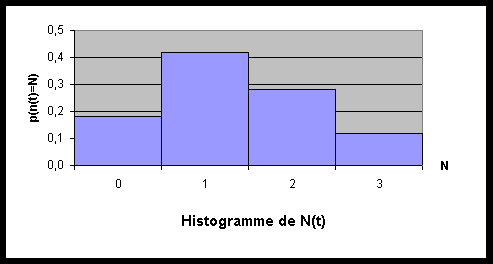
Distribution du nombre d'usagers
On peut aussi construire à partir d'une simulation un histogramme en vue d'une approximation de la densité d'une v.a. (ici le nombre d'usagers dans le système), ce qui permet, en principe, une caractérisation plus complète dont on peut déduire les estimations précédentes.
Un calcul simple établit la table des fréquences et donc une approximation des probabilités :
N |
Période dans laquelle N usagers sont dans le système. |
|
0 |
|
0,183 |
1 |
|
0,419 |
2 |
|
0,280 |
3 |
|
0,118 |
D'où l'histogramme suivant :
Dans cet exemple prototypique, nous nous proposons de simuler la variation du niveau d'un stock.
Considérons un entrepôt qui peut loger 10 unités d'engins encombrants et demandant des soins particuliers d'entretien. L'entrepôt est ouvert 5 jours par semaine. Chaque jour ouvrable, on peut recevoir 0, 1, 2, 3 ou 4 demandes d'achat ; les produits commandés seront livrés aux clients le jour même. On suppose que les demandes journalières sont indépendantes et que celles qui ne sont pas satisfaites seront passées à un concurrent. Une étude statistique montre que les probabilités de demandes journalières pour l'article sont réparties suivant la table suivante :
Nombre d'articles demandés dans une journée |
0 |
1 |
2 |
3 |
4 |
|
Probabilités |
0,3 |
0,3 |
0,2 |
0,1 |
0,1 |
0 |
Au soir d'un jour j où le niveau du stock n, tombe au-dessous de 4 unités (i.e. 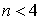 ) on passe une commande pour
) on passe une commande pour 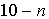 unités au fournisseur. Les produits commandés ne seront disponibles que le matin du jour
unités au fournisseur. Les produits commandés ne seront disponibles que le matin du jour 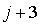 (samedis et dimanches exclus). Bien qu'une étude analytique complète du système en termes d'une chaîne de Markov soit possible, il semble qu'une simulation du niveau du stock soit aussi intéressante. Elle fournit en effet des informations sur la vraisemblance du modèle mathématique en effectuant une comparaison avec les données réelles et pourrait éventuellement aider à corriger le modèle, lorsque l'écart est jugé important.
(samedis et dimanches exclus). Bien qu'une étude analytique complète du système en termes d'une chaîne de Markov soit possible, il semble qu'une simulation du niveau du stock soit aussi intéressante. Elle fournit en effet des informations sur la vraisemblance du modèle mathématique en effectuant une comparaison avec les données réelles et pourrait éventuellement aider à corriger le modèle, lorsque l'écart est jugé important.
Simulons le modèle pendant 4 semaines, c'est-à-dire 20 jours ouvrables. Supposons qu'au matin du jour 1 le niveau du stock est de 10. Dans la simulation suivante, un tirage est effectué dans l'intervalle entier 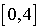 avec une distribution de probabilités décrites dans le tableau ci-dessus.
avec une distribution de probabilités décrites dans le tableau ci-dessus.
Il est possible, comme dans l'exemple précédent, de suivre pas à pas la construction de la suite d'événements résumés dans la table suivante :
Jour |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Niveau le matin |
10 |
8 |
7 |
7 |
7 |
3 |
1 |
7 |
6 |
6 |
4 |
4 |
2 |
1 |
8 |
5 |
3 |
3 |
9 |
8 |
Demande d'achat |
2 |
1 |
0 |
0 |
4 |
2 |
3 |
1 |
0 |
2 |
0 |
2 |
1 |
4 |
3 |
2 |
0 |
1 |
1 |
3 |
Niveau le soir |
8 |
7 |
7 |
7 |
3 |
1 |
0 |
6 |
6 |
4 |
4 |
2 |
1 |
0 |
5 |
3 |
3 |
2 |
8 |
5 |
Commande |
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
7 |
|
|
|
|
Les tirages effectués (simulant le nombre d'articles demandés) sont introduits en troisième ligne de la table. On notera que :
A la fin du 5ème jour, le niveau du stock étant tombé à 3, on passe donc une commande de réapprovisionnement de 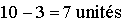 , qui ne seront disponibles que le matin du 8ème jour.
, qui ne seront disponibles que le matin du 8ème jour.
Le 7ème jour, il y a une disponibilité d'une unité le matin, alors que la demande est de 3. Il y a donc 2 demandes non satisfaites (colonne 7 marquée en rouge).
Des commandes de 8 et 7 unités ont été passées respectivement à la fin des 12ème et 16ème jour.
Les réapprovisionnements correspondants ont été effectués le 15ème et le 19ème jour.
Une perte de 3 demandes a été enregistrée à la fin du 14ème jour (marqué en rouge).
Cette suite d'événements permet d'estimer :
le niveau moyen du stock,
la distribution de probabilité pour le niveau du stock,
la fréquence de passage de commandes,
la répartition de quantité commandée,
la portion d'usagers perdus.
| |
Nous vous invitons à concevoir cette simulation dans un tableur et nous vous en proposons une ici dans EXCEL. |
| Microsoft Excel - 20,5Ko | |