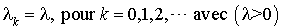
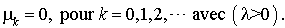
Processus de naissance pure de taux constant
Soit :
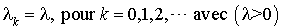
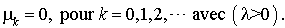
Le système d'équations différentielles de la proposition 1 devient :
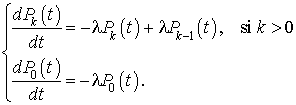
Si nous imposons la condition initiale 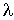 .
.
On a donc :
Processus de mort pure de taux constant
Soit :
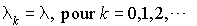
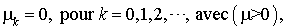
avec la condition initiale
Nous avons le diagramme de transitions suivant :
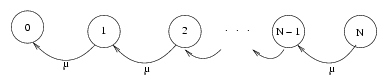
Le système d'équations différentielles qui détermine la distribution de probabilité s'écrit :
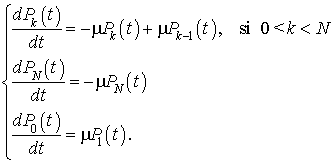
La seconde équation et la condition initiale 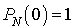 permettent d'obtenir une expression explicite pour
permettent d'obtenir une expression explicite pour 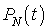 . On en déduit de proche en proche
. On en déduit de proche en proche 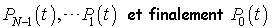 :
:
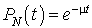
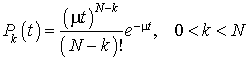
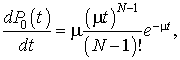 dont la solution est appelée la loi d'Erlang.
dont la solution est appelée la loi d'Erlang.
Processus naissance et de mort de taux constant
Soit :
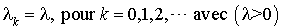
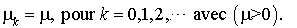
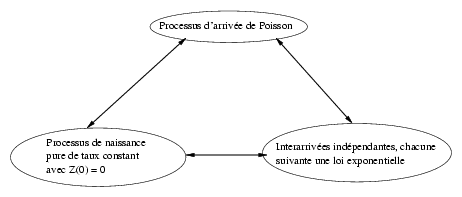
Ce processus modélise l'évolution d'une file d'attente à un seul serveur, lorsque le processus d'arrivée d'usagers est poissonnien et la durée de service est une v.a. exponentielle. Supposons en effet que le système d'attente satisfasse ces conditions.
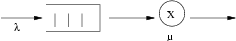
Nous avons alors :
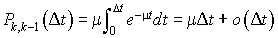
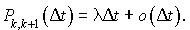
Nous pouvons donc tracer le schéma d'équivalence suivant :
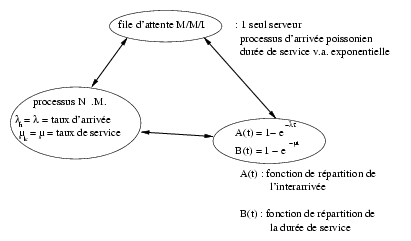
Le système d'équations différentielles s'écrit :
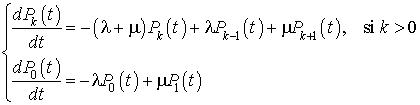
On peut résoudre ce système d'équations par la méthode des séries génératrices (ou par une transformation de Laplace). Dans la suite, nous nous limitons à une étude de la distribution stationnaire.