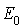 (taille 0), alors :
(taille 0), alors :Question 1 :
Pour qu'un processus de Markov homogène soit un processus de naissance et de mort :
Question 2 :
Dans tous les processus de naissance et de mort, lorsque le système est dans l'état 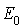 (taille 0), alors :
(taille 0), alors :
Question 3 :
Un processus de Poisson peut être considéré comme un processus de Markov démarrant à l'état 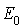 , avec le générateur infinitésimal étant la matrice infinie suivante :
, avec le générateur infinitésimal étant la matrice infinie suivante :
 |