Solution de l'exercice : Interarrivée généralisée
1. Nous avons :
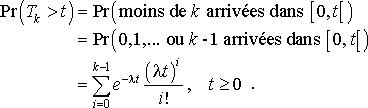
D'où :
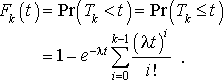
2. Cette fonction de répartition admet la densité :
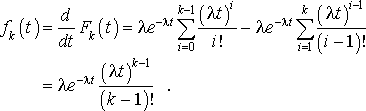
3.
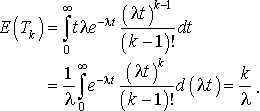
De façon analogue nous avons :
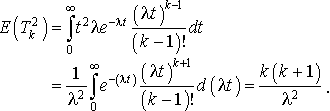
On en déduit :
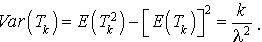
4. L'espérance mathématique et la variance de 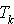 peuvent être calculées directement à partir de celles de la v.a.
peuvent être calculées directement à partir de celles de la v.a. 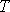 . En effet,
. En effet, 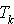 est la somme de
est la somme de 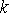 v.a. identiques et indépendantes, chacune d'espérance
v.a. identiques et indépendantes, chacune d'espérance 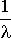 et de variance
et de variance 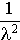 . L'espérance de
. L'espérance de 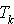 sera alors
sera alors  et sa variance
et sa variance 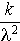 .
.
 |