Coding of Interval Routing

The routing information of a node is entirely determined by the knowledge of all the labels (its local name and the labels of its incident arcs). Implicitly, in the Interval Routing model one can permute the output ports numbers in advance. We mean that for the routing decision of a node x towards a destination y, x is able to determine the output port number such that $\cL(y) \in \cI(e)$, and to send the message onto this port (i.e., through the edge e) without extra information, excepted, of course, the knowledge of the label $\cI(e)$.

We invite the reader to see [BHV96] for a discussion of the impact of the node and/or port relabeling on routing information complexity. In all the following, the function $\log$ denotes the logarithm in base 2.

Let x be a node. For each $i \in \{1,\ldots,K\}$, we denote by [a_i,b_i] the i-th interval of x (with Condition 2b the intervals do not overlap), and by e_i the output port number on which is assigned this interval. First, we remark that only 2 intervals at most can be non-strict and/or cyclic. So, with an overhead of $O(\log{n})$ bits only, it is easy to implement any k-IRS, k-SIRS, or k-LIRS, from its strict and linear version.

W.l.o.g. we assume that the a_i's are sorted in increasing order, the intervals [a_i,b_i] are strict and linear, and we know the integers n, d, K, and $\cL(x)$ with an overhead of $5\log{n}$ bits². To code all the labels in x, it suffices to store the sequences $S_1=(a_1,\ldots,a_K)$ and $S_2=(e_1,\ldots,e_K)$. Indeed the b_i's can be computed as follows: If i<K, then b_i=a_i+1-1 (=a_i+1-2 if $\cL(x)=a_{i+1}-1$), otherwise b_K = n (=n-1 if $\cL(x)=n$). S₁ is a sequence of K distinct integers in the range 1 to n, therefore it can be stored with $\log{n \choose K}$ bits [LV93].

Let d be the number of output ports used by the IRS in x, i.e., $d = \vert\{e_i\mid 1 \leqs i \leqs K\}\vert$. The IRS does not use necessarily all the arcs incident to x, so d might be less than the degree of x. The number of ways to obtain S₂ is at most ${K \choose d} d^{K-d}$. Indeed, $S_2=(e_1,\ldots,e_K)$ is a sequence composed of exactly d different values e_i taken from $\{1,\ldots,d\}$ located in K possible places, and of K-d independent integers of $\{1,\ldots,d\}$. So, there is at most $d! {K \choose d}$ choices of the d different values of the sequences, and d^K-d ways for the K-d other elements; thus a total of $d! {K \choose d} d^{K-d}$ different sequences $(e_1,\ldots,e_K)$. However the permutation of the output ports numbers can be made in advance. Since d ports are used, at least d! sequences are equivalent up to a permutation of the ports, coding the same IRS. Each different IRS has a sequence S₂ which can be coded with $\log{(d!{K \choose d} d^{K-d}/d!)} = \log{K \choose d} + (K-d)\log{d}$ bits.

Thus the total number of bits used to store all the labels in x is bounded by $M = \log{n \choose K} + \log{K \choose d} + (K-d)\log{d} + c\log{n}$, for a suitable constant $c \leqs 5$. On the other hand, $k \leqs K \leqs dk$. Moreover ${n \choose K} \leqs (ne/K)^K \leqs (ne/k)^{dk}$, and $\log{K \choose d} \leqs K$. Hence

$$\log{n \choose K} + \log{K \choose d} ~\leqs ~ K\pare{\log{\... ...{n}{k}}+\log{(2e)}} ~\leqs ~ \log{(2e)}\, dk\log{\frac{n}{k}}.$$

We note that k is in the range $1 \leqs k \leqs n/2$, thus for n large enough, $(n/k)^k \geqs n$, and therefore $c\log{n} \leqs ck\log{(n/k)} \leqs c\,dk\log{(n/k)}$, for every constant $c \geqs 0$, and for every $d \geqs 1$. It follows that

$$\log{n \choose K} + \log{K \choose d} +c\log{n} ~\leqs ~ \pare{c+\log{(2e)}} dk \log{\frac{n}{k}}.$$

To prove that $M = O(dk\log{(n/k)})$, it remains to show that

$$(K-d)\log{d} \,\,\leqs \,\, \alpha\, dk \log{\frac{n}{k}}, \quad \mbox{for a suitable constant $\alpha \geqs 1$.}$$ (1)

Let assume that n > dk. In this case:

$$d < \frac{n}{k} \,\Rightarrow\, \log{d} < \log{\frac{n}{k}} ... ...ac{n}{k}} \,\Rightarrow\, (K-d)\log{d} < dk \log{\frac{n}{k}}.$$

It remains to show Inequality 1 for $n \leqs dk$. Let $\beta = dk/n$, $\beta \geqs 1$. Since $K \leqs n$, we get $K \leqs dk/\beta$. To show Inequality 1 it suffices to show:

$$\begin{eqnarray*} K\log{d} \leqs \alpha\, dk \log{\frac{d}{\beta}}, &\mbox{ or ... ...\Leftrightarrow&\, d \leqs \pare{\frac{d}{\beta}}^{\alpha\beta}. \end{eqnarray*}$$

Let $f(\beta) = (d/\beta)^{\alpha\beta}$. Thus, $f(\beta)$ increases if $f'(\beta) \geqs 0$ for $\beta \geqs 1$.

$$f'(\beta) = \alpha f(\beta)\pare{\ln\pare{\frac{d}{\beta}} - 1}.$$

$\alpha f(\beta) > 0$. Thus $f'(\beta) \geqs 0$ if $\ln{(d/\beta)} \geqs 1$, or $d \geqs \beta e$. So, if $d \geqs \beta e$ then $f(\beta) \geqs f(1) = d^{\alpha}$. Therefore if $d \geqs \beta e$ then Inequality 1 holds.

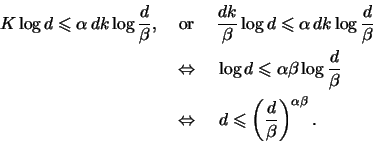
So, let us assume $d < \beta e$. If, furthermore, $\beta e \leqs \gamma\log{d}$, where $\gamma = 3/\log{3} \approx 1.892$, then it implies that $d < \gamma\log{d}$, which is impossible for $d \geqs 1$. So, $\beta e > \gamma\log{d}$. In this case it implies that:

$$\begin{eqnarray*} n \beta e \,>\, \gamma n\log{d} &\,\Rightarrow\,& dk e \,>\, ... ...K-d)\log{d} \,\,<\,\, \frac{e}{\gamma} \, dk \log{\frac{n}{k}}. \end{eqnarray*}$$

In total,

$$M \,<\, \pare{c+\log{(2e)} + \frac{e}{\gamma}} \,dk \log{\frac{n}{k}} \,<\, 9\,dk \log{\frac{n}{k}}.$$

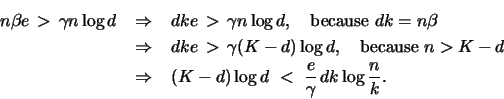
Theorem 1 implies that every 1-IRS (and its variants) can be coded with $n + O(\log{n})$ bits per node. Moreover, the implementation is quite easy using an n-bit vector coding within the 1's the left-boundary of each interval. The time complexity of the routing function is linear in n in this case (the time to locally compute the output port from any destination). However, adding a table of $\ceil{n/f(n)}$ integers, i.e., o(n) extra bits for some function f such that $\log{n} = o(f(n))$, the routing function can compute the output port in O(f(n)) bit-operations: Split the vector in $\ceil{n/f(n)}$ blocks of length at most f(n) bits, and tabulate for the ith block the number of 1's which is contained in the vector up to the position $i\point f(n)$.

One can even reduce the amount of bits needed to route for trees.

Let T be an n-node tree, and r be a node of T chosen as the root of T. For every edge (u,v), the graph obtained by removing (u,v) in T is composed of two connected components. We denote by T_(u,v) the component that contains v. We say that T_(u,v) is the subtree of T induced by (u,v). For all integers n,k, a k-partition of n is an integer sequence $(n_1,\ldots,n_k)$ such that $1 \leqs n_1 \leqs \ldots \leqs n_k$, and $\sum_{i=1}^k n_i = n$.

We label the nodes of T with a particular depth first search scheme as follows: We initialize the labeling process by labeling r with 1. For each node x, let $y_1, \ldots, y_k$ be the children of x ordered such that $\vert V(T_{(x,y_1)})\vert \leqs \ldots \leqs \vert V(T_{(x,y_k)})\vert$. We start to label recursively the subtrees $T_{(x,y_1)}, \ldots, T_{(x,y_k)}$ in this order. If $x \neq r$, we assign the output port number 1 to the edge towards r, i.e., the edge (x,y) with y the father of x, and for each $i \in \{1,\ldots,k\}$ the output port number i+1 to the edge (x,y_i). For x=r we assign the output port number i to the edge (x,y_i).

Consider a node $x \neq r$. We set $k=\deg(x)-1$, for each $i \in \{1,\ldots,k\}$, set n_i = |V(T_(x,yi))|, and finally we set $n_0 = n - \sum_{i=1}^k n_i$. We remark that $\sum_{i=0}^k{n_i} = n$, or equivalently $(n_1,\ldots,n_k)$ is a k-partition of n-n₀. We store in x:

itemize the label of x; the values n, n₀, and k; the k-partition of n-n₀: $(n_1,\ldots,n_k)$. itemize

For x = r we set $k=\deg(x)$, and n₀ = 1, and we store similarly the values n, k, and the k-partition of n-n₀ defined by $(n_1,\ldots,n_k)$. To simplify, x and y represent the labels of the node x and y respectively.

The routing scheme is the following: Assume the node x must route a message to the destination y. If x=y then the routing process ends. If $y \notin [x+1,x+n-n_0]$, then the message is forwarded to the father of x through the output port 1 (the case never happens if x = r). Otherwise, one computes the unique integer $p \geqs 1$ such that $y \in [x+1+\sum_{i=1}^{p-1}{n_i}, x+\sum_{i=1}^{p}{n_i}]$. The message is forwarded through the output port p+1, if $x \neq r$, and p for x = r. Clearly such a scheme corresponds to a 1-SIRS, because the union of all the intervals cover $\{1,\ldots,n\}$, and all the intervals are pairwise disjoint. Moreover they never contain x.

The process routes correctly. Indeed, by the construction of the node-labeling if $y \in [x+1+\sum_{i=1}^{p-1}{n_i}, x+\sum_{i=1}^{p}{n_i}]$, then y is necessarily a node of the subtree T_(x,yp), and the output port assigned to the edge (x,y_p) is p+1 if $x \neq r$, and p if x = r. And if $y \notin [x+1,x+n-n_0]$, then y is not a descendent of x, and hence must be forwarded to its father.

Let us compute the amount of information required. The integer values of n, n₀, k, and the label of x can be stored using $O(\log{n})$ bits. Knowing n and k, any k-partition of n, P, can be coded using at most $\ceil{\log{U_n}}$ bits, where U_n is the total number of partitions of n. Indeed, there exists very simple algorithm that, knowing n, enumerates all the partitions of n. So, it suffices to store the index of P in such an enumeration. Furthermore, we have the well-known formula due to Harder and Ramanujan in 1917 [Hal86, Equation (4.2.7) page 44]:

$$U_n ~\sim~ \frac{1}{4n \sqrt{3}}\, e^{\pi\sqrt{2n/3}}.$$

Globally $3.71\sqrt{n}$ bits per node suffice to describe the routing algorithm for n large enough, that completes the proof.

Note that in [EGP98], it is shown that to route in an arbitrary n-node tree $\Omega(\sqrt{n})$ bits are required, showing that the bound of Theorem 2 is tight.

We remark that the distinction between the variants of Interval Routing has no real impact on the coding of IRS in local memory of the nodes, up to an additive term of $O(\log{n})$ bits. The interest of these variants will appear in Theorem 43 of Section 3.8.

Since every edge needs $O(k\log{n})$ bits of information to code its labels, the total amount of routing information for the entire graph G=(V,E) is bounded by $O(\vert E\vert k\log{n})$ bits.