- ...that1
- $2^(V)$ denotes the power set
of $(V)$, i.e., the set of all the subsets of
${1,...,|V|}$.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
bits2
-
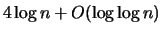 bits suffice to store n,
d, K,
bits suffice to store n,
d, K, 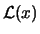 in a self-delimiting way, which is bounded by
in a self-delimiting way, which is bounded by
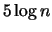 for n large enough.
for n large enough.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...odd3
- The Theorem was unfortunately mistyped in the original
paper. Here, we give the correct statement.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...triangulated4
- A plane graph where all the
faces are triangles.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 5
5
- The original result presented in
this article is $2$-$ dilation(multi-globe) 1.25D$.
However in the construction given in the proof it appears that the
number of intervals is 3. To our best knowledge we do not know
whether it can be done with 2 intervals only.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
graph6
- I.e.,
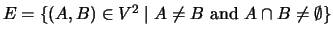 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.