Tas

Un tas est un arbre binaire dans lequel chaque nud est inférieur ou égal à tous ses descendants, selon un ordre défini par le domaine des éléments stockés dans l'arbre. De plus, chaque niveau de l'arbre doit être rempli de gauche à droite, une propriété définie plus formellement comme suit :

• la racine de l'arbre est étiquetée 0,
• le fils gauche d'un nud étiqueté n, est étiqueté 2n+1,
• le fils droit d'un nud étiqueté n, est étiqueté 2n+2.

Ces étiquettes sont fixes et distinctes des éléments stockés dans les nuds.

Un arbre t est un tas si et seulement si :

• pour chaque nud N de t, l'élément de N est supérieur ou égal à celui du parent de N,
• si un nud N avec une étiquette n existe dans t, alors tous les nuds avec une étiquette inférieure à n existent aussi.

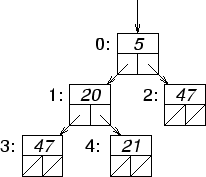
La figure 23.20 montre un exemple de tas, alors que l'arbre des figures 23.21 et 23.22 montrent des arbres qui n'en sont pas. En effet, l'arbre de la figure 23.21 ne respecte pas la première condition et celui de la figure 23.21 ne respecte pas la deuxième. Le domaine utilisé est les entiers et l'ordre est déterminé par la fonction Common Lisp <.

Figure 23.20: Exemple d'un tas

Figure 23.21: Exemple d'un arbre qui n'est pas un tas

Figure 23.22: Exemple d'un arbre qui n'est pas un tas

Grâce à la deuxième condition ci-dessus, un tas peut être représenté sous la forme d'un vecteur. L'indice de l'élément correspond à l´étiquette. L'insertion d'un élément dans un tas doit être faite après le dernier élément existant, et seul le dernier élément du vecteur peut être supprimé. L'insertion ou la suppression d'un élément peut bien sûr nécessiter l'expansion ou la contraction du vecteur de la même façon que dans la section 23.3.2.

Mais l'insertion d'un élément après le dernier élément ne préserve pas forcément la première condition. Pour corriger ce problème, après l'insertion on échange l'élément ainsi insérer avec son parent tant que ce dernier est supérieur aux éléments insérés. La figure 23.23 montre l'insertion de l'élément 3 dans le tas de la figure 23.20.

Figure 23.23: Insertion dans un tas

La suppression d'un élément dans un tas ne peut se faire que si l'on connaît sa place, à savoir l'étiquette du nud dans lequel il se trouve. La recherche d'un élément quelconque dans un tas peut nécessiter O(n) opérations où n est le nombre d'éléments dans le tas. La raison est que, contrairement à un arbre binaire de recherche, la racine d'un sous-arbre d'un tas ne donne aucune indication concernant le sous-arbre dans lequel se trouve l'élément. La recherche étant un prérequis à la suppression d'un élément arbitraire, une suppression peut nécessiter O(n) opérations aussi.

La suppression d'un élément dont la place est connue peut provoquer un non respect de la deuxième condition ci-dessus. La solution de ce problème est d'abord d'échanger l'élément de cette place et celui de la dernière place, puis de supprimer l'élément de la dernière place, ce qui respecte la deuxième condition. Mais comme pour l'insertion, la première condition n'est alors pas forcément respectée. La solution est similaire :

• si l'élément est inférieur à son parent, échanger avec le parent,
• sinon, échanger avec le plus petit de ses fils

et répéter tant que l'arbre n'est pas un tas.

La figure 23.24 montre la suppression de l'élément 20 (sur la place numéro 1) du dernier tas de la figure 23.23. Cet élément est d'abord échangé avec l'élément 47 de la dernière place (place numéro 5), puis l'élément de la place numéro 5 est supprimé conformément au respect de la deuxième condition. Puis l'élément 47 de la place numéro 1 est échangé avec l'élément 21 de la place 4 pour rétablir la première condition.

Figure 23.24: Suppression dans un tas

Les opérations d'échange sont particulièrement efficaces, car le calcul de l'indice peut se faire avec des instructions de décalage et d'addition uniquement. Aucune multiplication n'est nécessaire.

Pour l'implémentation du tas, nous allons utiliser les fonctions définies dans la section 23.3.2 et qui permettent d'obtenir automatiquement l'expansion et la contraction en cas de besoin.

Voici la fonction d'insertion :

(defun heap-insert (element heap &key (test #'<) (key #'identity))
  (vector-insert element heap)
  (loop for i = (1- (length heap)) then nexti
        for nexti = (ash (1- i) -1)
        while (> i 0)
        while (funcall test
                       (funcall key (aref heap i))
                       (funcall key (aref heap nexti)))
        do (rotatef (aref heap i) (aref heap nexti)))
  heap)

Exercice : écrire la fonction de suppression.

Exercice : modifier la fonction de création d'un tas pour qu'elle tienne compte du type d'éléments et de la taille initiale du vecteur à créer.

Exercice : le cas du tas est l'un des rares où un vecteur dont le premier élément a l'indice 1 pourrait être avantageux. Réécrire les fonctions de manipulation d'un tas pour qu'elles n'utilisent pas le premier élément du vecteur en simplifier autant que possible le code.

On peut s'interroger sur l'utilité d'un tas si la recherche d'un élément arbitraire est si coûteuse. En fait, cette structure est utile entre autre pour le tri (voir section 24.3.1) et pour implémenter les files de priorité (voir section 28.6).