 |
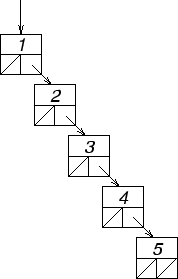
Le problème principal avec les arbres binaires de recherche est qu'il n'y a aucune garantie que l'arbre soit équilibré, à savoir que les hauteurs de chacun des sous-arbres soit à peu près égales. Une suite malheureuse d'insertions ou de suppressions peut provoquer un arbre ayant la forme d'une liste plutôt que d'un arbre. Dans ce cas, les opérations ne sont plus de complexité O(log n), mais O(n). Voir la figure 23.13 pour le résultat de l'insertion de la suite 1, 2, 3, 4, 5 dans un arbre binaire de recherche.
La consommation de mémoire peut être un autre problème. Pour chaque élément, il y a un surcoût de trois pointeurs plus l'en-tête, soit environ quatre pointeurs. C'est à comparer avec un seul pointeur pour le vecteur par exemple. L'utilisation d'un arbre pour stocker de petits objets comme des caractères provoque donc un surcoût d'un facteur 15 à 30 selon la taille d'un pointeur de la machine. De plus la consommation de mémoire peut être un problème pour le cache si ce dernier n'est pas assez grand.
La quantité de cellules, une pour chaque élément stocké, peut ralentir le ramasse-miettes. Celui-ci doit effectivement tracer chaque cellule récursivement.
Le ramasse-miettes risque de disperser les cellules en mémoire, ce qui peut conduire à des défauts de cache. Ce problème devrait pourtant rester relativement mineur, car le nombre de cellules parcourues est souvent relativement faible.