Université Bordeaux 1

Arbre 2-3 et B Arbres

---

• Arbre 2-3
• (a-b)-arbres
• Structure de données et primitives

2-3 Arbres

Définition 10.1.Soit k un entier. On appelle k-noeud un noeud qui a k fils.

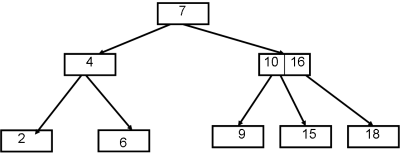
Définition 10.2.Un arbre 2-3 est un arbre équilibré éventuellement vide tel que tout noeud à 2 ou 3 fils et vérifiant :

• la valeur des clés est contenue dans les feuilles
• un 2-noeud contient la valeur r
  • le fils gauche donne accès à des valeurs inférieures ou égales à r
  • le fils droit à des valeurs supérieures strictement à r
• un 3-noeud contient deux valeurs r et s,
  • le fils gauche donne accès à des valeurs inférieures ou égales à r
  • le fils du milieu donne accès à des valeurs dans l'intervalle ]r,s]
  • le fils droit à des valeurs supérieures strictement à s



Insertion

L'insertion se fait sur une feuille de l'arbre.
• la feuille s'insère sur un 2-noeud, on transforme le 2-noeud en 3-noeud.
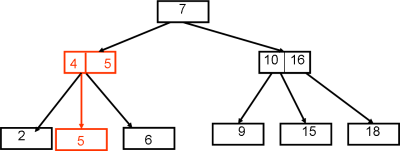
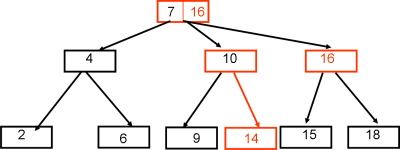
• la feuille s'insère sur un 3-noeud, on transforme le 3-noeud en deux 2-noeud. On répète l'opération en remontant dans l'arbre si nécessaire.
Un arbre 2-3 s'étire donc en hauteur par la racine.

Suppression

C'est une feuille de l'arbre que l'on supprime. Elle a un père p
• si p est un 3-noeud alors p devient un 2-noeud
• si p est un 2 noeud, on procède en fonction du grand-père de la feuille g=pere(p)
  • si le grand-père est un 3-noeud, on fusionne un fils avec p si c'est un 2 noeud sinon on casse ce fils et on fusionne un de ses fils avec p
  • si le grand-père est un 2-noeud, si le fils "proche" de p est un 3-noeud on fusionne son fils ainé avec p sinon on fusionne ce noeud avec p et on recommence sur le grand-père qui devient un noeud a fils unique.
  (voir ici)
  (voir des exemples)
  

---

(a-b)-arbres

Définition 10.3.Un (a,b)- arbre est un arbre étiquetté qui vérifie :

• La racine est une feuille ou possède au moins 2 fils.
• Tout noeud interne possède entre a et b fils.
• Toutes les feuilles sont au même niveau

De plus

• Les noeuds internes sont de la forme (a₀, k₁, a₁, k₂,..., k_b-1, a_b-1) avec a_i pointeur vers un sous arbre et k_i sont des valeurs,
• k₁ < k₂ <... < k_b
• les valeurs des feuilles du sous arbre pointé par a_i-1 sont inférieures ou égales à k_i,
• les valeurs des feuilles du sous arbre pointé par a_i+1 sont supérieures à k_i,

Les 2-3 arbres sont des cas particuliers de a-b arbres. Le plus souvent on choisit b=2a-1. On parle alors de B-arbres. Une variante consiste a autoriser les clés dans les noeuds internes.

---

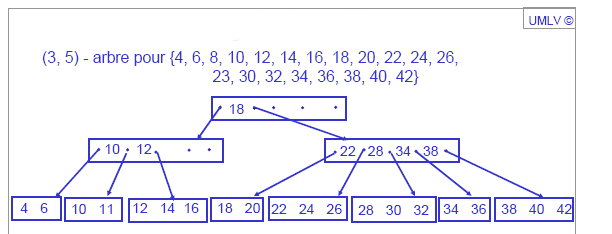
(voir des exemples)


Structure de données et primitives

Les B-arbres sont des containeurs. Dans les B-arbres, il est important de garder des acccès rapides aux fils et de remonter aisément dans l'arbre. On utilise la structure suivante.

sommet=^cellule;
celluleUnitaire=structure
        clé:objet;
        fils:sommet;
finstructure

cellule=structure
          premierFils:sommet;
          autreFils:tableau[a..b] de celluleUnitaire
          frere:sommet;
          pere:sommet;
finstructure;