



Next: About this document ...
Up: Les systèmes distribués
Previous: Les systèmes de fichiers
Index
Subsections
Le besoin de synchroniser et de faire communiquer des processus existe
également dans un système réparti.
Il est nécessaire, pour traiter un certain nombre de problèmes,
d'avoir un ordre global sur les événements d'un système.
Peut être construit à partir de : adresse machine, numéro de
processus, horloge locale.
Problème : pas cohérent (du fait des dérives) avec l'envoi et la
réception de messages.
UTC : Temps Universel Coordonné suffit pour beaucoup de problèmes
(dates des fichiers ...), mais insuffisant pour section critique,
interblocages...car les délais de transmission ne sont pas connu
exactement.
Une relation 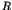 telle que :
telle que :
- Pour chaque processus
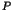 , si
, si 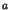 est antérieur à
est antérieur à 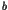 , alors
, alors
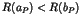
- Pour chaque couple de processus
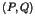 , si
, si 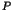 envoie à
envoie à 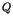 un
message
un
message 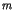 , alors
, alors
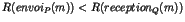
L'algorithme de Lamport :
- A chaque création de processus
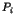 , initialiser un compteur
, initialiser un compteur
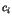 à 0.
à 0.
- A chaque événement significatif de
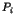 , incrémenter
, incrémenter 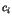 .
.
- Estampiller chaque envoi de message
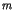 par
par 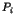 du compteur
du compteur
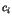 .
.
- A chaque réception de message
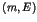 par un processus
par un processus 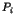 ,
celui ci effectue l'opération
,
celui ci effectue l'opération
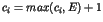 .
.
Un coordinateur : 3 messages par entrée (éventuellement un
acquittement de la demande).
Pb : si le coordinateur tombe en panne.
Une solution basée sur les horloges logiques avec
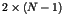 messages par entrée en section critique.
messages par entrée en section critique.
Un jeton matérialise l'accès à la section critique. Le jeton circule de processus en processus généralement sur un circuit.
Le problème de l'interblocage
Les solutions vues au chapitre sur l'interblocage sont plus ou moins adaptables :
- Exclusion mutuelle :
- on utilise un spool pour toutes les ressources qui le permettent.
- Tenir et attendre :
- un protocole à deux phases est souvent mis en place pour les transactions dans les SGBD.
- Pas de réquisition :
- la solution proposée (un processus déclare réquisitionnables ses variables) ne peut pas s'appliquer à toutes les ressources, et peut provoquer la famine.
- Attente circulaire :
- la solution de l'ordre sur les ressources du réseau est difficile à mettre en
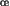 uvre.
uvre.
L'algorithme suivant qui utilise des horloges logiques permet un contrôle des réquisitions qui ne provoque pas de famine.
L'idée est la suivante :
- A chaque processus
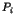 est associée une estampille
est associée une estampille 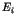 qui correspond à son instant de création.
qui correspond à son instant de création.
- L'estampille détermine la priorité du processus, afin qu'un processus retardé deviennent de plus en plus prioritaire.
Il existe deux schémas de mise en 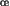 uvre :
uvre :
- wait-die (attendre-mourir)
- n'utilise pas la réquisition.
Dans ce schéma, si
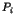 désire une ressource détenue par
désire une ressource détenue par 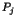 deux cas :
deux cas :
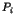 attend (un certain temps) si
attend (un certain temps) si 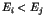 .
.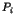 meurt (il rend ses ressources un certain temps) si
meurt (il rend ses ressources un certain temps) si 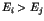 .
.
- wound-wait (blessé-attendre)
- utilise la réquisition.
Dans ce schéma, si
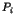 désire une ressource détenue par
désire une ressource détenue par 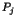 deux cas :
deux cas :
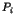 attend (un certain temps) si
attend (un certain temps) si 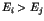 .
.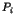 blesse
blesse 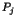 (il le force à rendre ses ressources) si
(il le force à rendre ses ressources) si 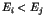 .
.
Ces schémas sont sans famine si les processus blessés et morts recommencent avec la même estampille après un délai qu'il faut estimer, mais peuvent être très inefficaces.
La détection consiste toujours à trouver un cycle dans le graphe d'allocation des ressources.
Il est facile pour chaque site 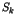 de maintenir un graphe d'attente local qui contient tous les arcs
de maintenir un graphe d'attente local qui contient tous les arcs 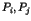 dès que
dès que 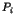 (local ou non) désire une ressource
(local ou non) désire une ressource 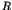 du site
du site 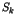 , tenue par
, tenue par 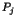 (local ou non).
(local ou non).
Ces graphes vérifient les propriétés :
- si l'un deux possède un cycle, il y a un interblocage.
- il n'y a pas d'interblocage si l'union de l'ensemble des graphes est sans cycle.
Il est donc nécessaire de construire le graphe d'attente global.
d'interblocage.
![\begin{automate}[t]{400}{150}{Les graphes d'attentes locaux et l'union}{1}
\etat...
...}{un}{}
\par\trans[d]{trois}{quatre}{}
\trans{quatre}{deux}{}
\par\end{automate}](img101.gif)
Un processus coordonnateur est chargé de gérer le graphe global. Celui-ci peut être maintenu en permanence ou bien calculer périodiquement.
Le défaut majeur est qu'il est impossible d'avoir le graphe réel du fait du temps pris par les communications. Une des conséquences est la détection de faux interblocages (une libération est arrivée trop tard).
Soit la situation suivante :
![\begin{automate}[t]{400}{150}{Les graphes d'attentes locaux et le graphe global}...
...{trois}{quatre}{}
\par\trans[d]{sept}{cinq}{}
\trans{cinq}{six}{}
\end{automate}](img102.gif)
Supposons maintenant le scénario suivant :
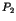 libère la ressource du premier site.
libère la ressource du premier site.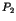 demande une ressource du second site tenue par
demande une ressource du second site tenue par 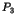
et enfin supposons que du fait du réseau le message de la demande arrive au coordinateur avant le message de libération. La situation est alors :
![\begin{automate}[t]{250}{150}{Un faux interblocage}{1}
\etat{50}{100}{$P_1$}{un}...
...ar\trans[d]{sept}{cinq}{}
\trans{cinq}{six}{}
\trans{six}{sept}{}
\end{automate}](img104.gif)
Il existe des solutions centralisées basées sur les horloges logiques.
Chaque site 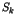 maintient un graphe composé de :
maintient un graphe composé de :
- Les arcs
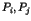 dès que
dès que 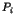 (local ou non) désire une ressource
(local ou non) désire une ressource 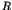 du site
du site 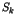 , tenue par
, tenue par 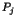 (local ou non).
(local ou non).
- Les arcs
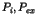 dès que
dès que 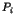 local désire une ressource d'un autre site, tenue par un processus quelconque non local.
local désire une ressource d'un autre site, tenue par un processus quelconque non local.
- Les arcs
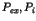 dès que
dès que 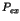 non local désire une ressource
non local désire une ressource 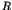 du site
du site 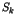 , tenue par
, tenue par 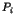 (local ou non).
(local ou non).
Dans ce graphe une attente d'un processus 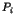 non local sur une ressource locale détenue par
non local sur une ressource locale détenue par 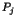 apparaît deux fois :
apparaît deux fois : 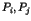 et
et 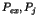
Ce graphe possède les propriétés :
- si l'un deux possède un cycle sans
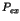 , il y a un interblocage.
, il y a un interblocage.
- si l'un deux possède un cycle avec
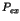 , il y a risque d'interblocage.
, il y a risque d'interblocage.
Dans le second cas, notons
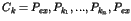 le cycle du site
le cycle du site 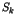 . Il faut noter que le site
. Il faut noter que le site 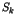 connaît exactement la composition de
connaît exactement la composition de 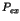 qui débute le cycle, mais pas celle de
qui débute le cycle, mais pas celle de 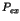 qui termine le cycle.
Le site déclenche l'algorithme suivant :
qui termine le cycle.
Le site déclenche l'algorithme suivant :
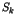 communique le cycle
communique le cycle 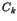 au site
au site 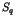 qui détient la ressource convoitée par le processus
qui détient la ressource convoitée par le processus 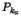 ;
;- le site
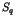 met à jour son graphe. Trois cas :
met à jour son graphe. Trois cas :
- il n'existe pas de cycle, il n'y a pas d'interblocage.
- il existe un cycle sans
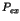 , il y a un interblocage.
, il y a un interblocage.
- il existe un cycle avec
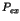 , le site
, le site 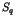 continue l'algorithme de détection vers un nouveau site.
continue l'algorithme de détection vers un nouveau site.
- les
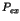 sont à chaque itération de moins en moins nombreux, il y a donc un site sur lequel l'algorithme s'arretera, et qui conclura par interblocage ou non.
sont à chaque itération de moins en moins nombreux, il y a donc un site sur lequel l'algorithme s'arretera, et qui conclura par interblocage ou non.
En fait, s'il y a interblocage distribué, plusieurs sites vont posséder un cycle local avec 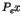 , il est donc inutile que tous déclenchent l'algorithme. Une optimisation possible utilise un ordre sur les processus :
, il est donc inutile que tous déclenchent l'algorithme. Une optimisation possible utilise un ordre sur les processus :
- le site
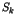 observe le cycle
observe le cycle
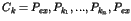 ,
,
- le site
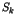 déclenche l'algorithme si et seulement si
déclenche l'algorithme si et seulement si 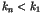 .
.
Considérons la situation du vrai interblocage initial. Supposons que :
- les processus
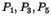 sont du site
sont du site 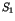 ,
,
- les processus
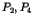 sont du site
sont du site 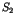 ,
,
- les arcs localisent les ressources.
Nous avons alors :
![\begin{automate}[t]{350}{150}{Les graphes d'attentes locaux}{1}
\etat{50}{100}{$...
...\etat{230}{50}{$P_{ex}$}{pex}(40,20)
\trans[acw]{sept}{pex}{}
\par\end{automate}](img119.gif)
L'algorithme produit :
- Les deux sites constatent un cycle :
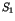 voit le cycle
voit le cycle
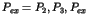 ,
,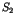 voit le cycle
voit le cycle
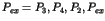 ,
,
- le site
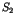 envoie à
envoie à 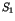 le cycle
le cycle
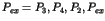 ,
,
- le site
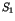 met à jour son graphe.
met à jour son graphe.
- le site
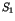 détecte l'interblocage.
détecte l'interblocage.
On peut citer :
- L'Atomicité :
- les transactions sont des suites d'actions qui n'en font qu'une. C'est à dire que soit toutes les actions terminent, soit aucune. Les actions peuvent concernées des ressources et des processus sur plusieurs sites. La solution la plus souvent mise en
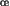 uvre est le protocole de validation à deux phases.
uvre est le protocole de validation à deux phases.
- L'élection :
- de nombreux algorithmes répartis utilisent un coordinateur. Celui-ci peut tomber en panne, il est alors nécessaire d'initialiser un nouveau coordinateur. Le problème est complexe car :
- il faut être certain que le coordinateur est en panne,
- il faut connaître tous les coordinateurs potentiels.
Une solution est basée sur :
- un processus qui pense que le coordinateur est en panne se proclame nouveau coordinateur, et diffuse l'information à ses voisins;
- un processus qui reçoit un message d'élection participe à l'élection, soit il sait que le coordinateur n'est pas en panne, soit il accepte le nouveau coordinateur, soit il se déclare nouveau coordinateur car il est prioritaire au processus qui lui à envoyer le message. Le processus diffuse cette nouvelle information;
- un processus est élu lorsqu'il à reçu un accord de tous ses voisins.




Next: About this document ...
Up: Les systèmes distribués
Previous: Les systèmes de fichiers
Index
Alain GRIFFAULT
2000-12-22
![]() telle que :
telle que :
![]() messages par entrée en section critique.
messages par entrée en section critique.
![]() uvre :
uvre :
![]() de maintenir un graphe d'attente local qui contient tous les arcs
de maintenir un graphe d'attente local qui contient tous les arcs ![]() dès que
dès que ![]() (local ou non) désire une ressource
(local ou non) désire une ressource ![]() du site
du site ![]() , tenue par
, tenue par ![]() (local ou non).
(local ou non).
![\begin{automate}[t]{400}{150}{Les graphes d'attentes locaux et l'union}{1}
\etat...
...}{un}{}
\par\trans[d]{trois}{quatre}{}
\trans{quatre}{deux}{}
\par\end{automate}](img101.gif)
![\begin{automate}[t]{400}{150}{Les graphes d'attentes locaux et le graphe global}...
...{trois}{quatre}{}
\par\trans[d]{sept}{cinq}{}
\trans{cinq}{six}{}
\end{automate}](img102.gif)
![\begin{automate}[t]{250}{150}{Un faux interblocage}{1}
\etat{50}{100}{$P_1$}{un}...
...ar\trans[d]{sept}{cinq}{}
\trans{cinq}{six}{}
\trans{six}{sept}{}
\end{automate}](img104.gif)
![]() maintient un graphe composé de :
maintient un graphe composé de :
![]() non local sur une ressource locale détenue par
non local sur une ressource locale détenue par ![]() apparaît deux fois :
apparaît deux fois : ![]() et
et ![]()
![]() le cycle du site
le cycle du site ![]() . Il faut noter que le site
. Il faut noter que le site ![]() connaît exactement la composition de
connaît exactement la composition de ![]() qui débute le cycle, mais pas celle de
qui débute le cycle, mais pas celle de ![]() qui termine le cycle.
Le site déclenche l'algorithme suivant :
qui termine le cycle.
Le site déclenche l'algorithme suivant :
![]() , il est donc inutile que tous déclenchent l'algorithme. Une optimisation possible utilise un ordre sur les processus :
, il est donc inutile que tous déclenchent l'algorithme. Une optimisation possible utilise un ordre sur les processus :
![\begin{automate}[t]{350}{150}{Les graphes d'attentes locaux}{1}
\etat{50}{100}{$...
...\etat{230}{50}{$P_{ex}$}{pex}(40,20)
\trans[acw]{sept}{pex}{}
\par\end{automate}](img119.gif)