Efficiency of Interval Routing: Dilation and Stretch Factor

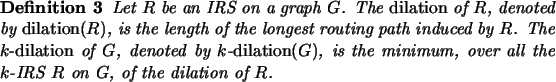
Whereas compactness, linearity, and strictness are qualitative parameters of the labeling, we can also define several other criteria to measure the quality of the routing induced by the IRS. Here the graphs considered have uniform weights on all the links.

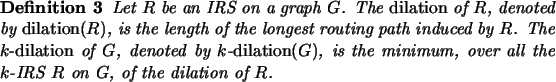
$\begin{definition} Let $R$\ be an IRS on a graph $G$. The {\em dilation\/} of $... ...mum, over all the $k$-IRS $R$\ on $G$, of the dilation of $R$. \end{definition}$

By taking a labeling like a depth first search along a minimum spanning tree, the result of [SK85] implies that every graph G of diameter D satisfies 1- $\mbox{\rm dilation}(G) \leqs 2D$ (more precisely, twice the radius of G). Moreover, by combining Theorem 2, we can conclude that every graph of diameter D has a 1-SIRS of dilation at most 2D which can be implemented with $O(\sqrt{n})$ bits in each router.

First, let us emphasize that the behavior between 1-IRS and 1-LIRS is different for the dilation.

$\begin{theorem}[\cite{EMZ96}] For every fixed $D$, there exists a graph $G$\ of... ...east $D^2/18$. Moreover $G$\ is planar and of maximum degree~$4$. \end{theorem}$

The following result of [TL97b] shows that the IRS proposed by [SK85] based on a spanning tree is close to the optimal.

$\begin{theorem}[\cite{TL97b}] For every even $D$, there is a graph $G$\ of diam... ...of girth $2D$, such that $1$-$\mbox{\rm dilation}(G) \geqs 2D-3$. \end{theorem}$

However, allowing more than one interval per edge, it is possible to decrease the dilation.

$\begin{theorem}[\cite{KRS97}] For every $n$-node graph $G$\ of diameter~$D$, th... ...n}}}+1$\ such that $k$-$\mbox{\rm dilation}(G) \leqs \ceil{3D/2}$. \end{theorem}$

Combined with the result of [GP97] (cf. the remark of Theorem 15), it is possible to improve the labeling of the regions defined in the proof of [KRS97a] in order to show that actually one can choose $k \leqs \frac{1}{4}\sqrt{n\ln{n}} + O(n^{1/4}\log^{3/4}{n})$ .

$\begin{theorem}[\cite{Gav97}] For every $D \geqs 2$, there exists an $n$-node g... ...ery $k \leqs cn/(D\log{(n/D)})$, and for a suitable constant $c$. \end{theorem}$

It should be noted that the dilation is quite sensitive to the additive term around 3/2 the diameter.

$\begin{theorem}[\cite{FN97}] For every $D \geqs 4\log{n}$\ there exists an $n$-... ...3D/2 - 2\log{(n/D)}$, for every $k \leqs 0.05\,n/(D\log{(n/D)})$. \end{theorem}$

Open question 1
- Is the lower bound $\Omega(D^2)$ for the dilation of 1-LIRS tight?
- What is the smallest integer k (as function of n and D) such that k- $\mbox{\rm dilation}(G) \leqs \ceil{3D/2}$ , for every n-node graph G of diameter D?

Although, using a 1-IRS based on depth first search, the routing path lengths remains always linear in the diameter, this length might be very large for nodes that are relatively close.

$\begin{definition} Let $R$\ be an IRS on a graph $G$. The {\em stretch factor\/... ...ver all the $k$-IRS $R$\ on $G$, of the stretch factor of $R$. \end{definition}$

In practice we are interested in designing k-IRS with the smallest possible stretch factor. So, IRS of stretch factor 1 is of special interest.

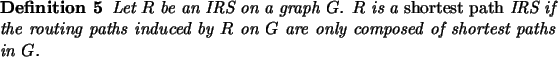
$\begin{definition} Let $R$\ be an IRS on a graph $G$. $R$\ is a {\em shortest p... ...ed by $R$\ on $G$\ are only composed of shortest paths in $G$. \end{definition}$

$\begin{definition} The {\em compactness\/} of a graph $G$, denoted by $\mbox{\r... ...t integer $k$\ such that $G$\ supports a shortest path $k$-IRS. \end{definition}$

The compactness of G=(V,E) is called sometimes the IRS number of G. As we saw previously the space complexity for the storage of a routing scheme in x is $O(dk\log{(n/k)})$ bits or $O(\vert E\vert k\log{n})$ bits in total. Therefore the compactness, k, is an important parameter in the design of compact routing schemes.

We can define similarly the linear compactness ( $\mbox{\rm LIRS}(G)$ ) and the strict or strict-linear compactness ( $\mbox{\rm SIRS}(G)$ and $\mbox{\rm SLIRS}(G)$ ) of graphs. However, up to an additive constant these variants are equivalent.

$\begin{definition} Let $R$\ be an IRS on a graph $G$, and $t \geqs 0$\ be an in... ...node $y$\ at distance at most $t$\ of $x$\ are shortest paths. \end{definition}$

The dilation of any t-regional IRS is at most n-(t+1), if n-(t+1) > t+1, i.e., if $n \geqs 2t + 3$ . So, the stretch factor of a t-regional IRS is at most n/(t+1) - 1.

$\begin{theorem}[\cite{vLT87}] \mbox{} \beginsmall{itemize} \par\item Every $n$-n... ... $1$-$\mbox{\rm stretch}(H) \leqs n/2 - 1$. \par\endsmall{itemize} \end{theorem}$

Open question 2
- Is there an n-node graph G, for every n large enough, such that 1- $\mbox{\rm stretch}(G) = \Omega(\sqrt{n})$ ? (The best known lower bound is a constant. It is derived from the result of [TL97a] showing the construction of a graph G such that 1- $\mbox{\rm stretch}(G) \geqs 7$ ).
- What are the general bounds for k- $\mbox{\rm stretch}(G)$ , k > 1?
- Do all graphs support a 1-regional 1-IRS?

We will see that there is no hope to extend Theorem 11 to 2-regional IRS. Indeed in Paragraph 3.1, Theorem 16 states that shortest path IRS in n-node graphs of diameter 2 require n/4 - o(n) intervals in the worst-case. The 2-regional linear IRS satisfy the following property:

$\begin{theorem}[\cite{ZTRP94}] If $G$\ supports a $2$-regional $1$-SLIRS then e... ... is either a bridge, or belongs to a cycle of length~$3$\ or~$4$. \end{theorem}$

The parameters dilation and stretch factor do not necessary reflect the quality of a routing scheme. The density of long routing paths may be small. We believe that for a better analysis of the real networks it would be relevant to consider the average dilation and the average stretch factor.

In the next definition $\rho(x,y)$ denotes the routing path length induced by the routing scheme R from x to y, and s(x,y) the ratio between $\rho(x,y)$ and the distance between x and y.

$\begin{definition} Let $R$\ be an IRS on an $n$-node graph $G$. The {\em averag... ...on $G$, of the average dilation of $R$\ (\resp stretch factor). \end{definition}$

The average stretch factor has been studied for Interval Routing in 2D-grids in [SML94]. For general graphs we have:

$\begin{theorem}[\cite{EGP98a}] For every $n$-node weighted graph $G$\ of diamet... ...ilation is at most~$\ceil{3D/2}$\ if all the weights are uniform. \end{theorem}$

Open question 3
- What are the bounds on average dilation and average stretch factor of k-IRS for arbitrary graphs?