A chordal ring is an augmented ring, or a circulant graph with
a chord of length 1. Formally it is defined by the pair (n,L) where
n is the number of nodes of the ring, and L is the set of chords,
![]() .
Each chord
.
Each chord ![]() connects
every pair of nodes of the ring that are at distance l in the ring.
We denote by
connects
every pair of nodes of the ring that are at distance l in the ring.
We denote by
![]() ,
,
![]() ,
the
chordal ring defined by
,
the
chordal ring defined by
![]() .
The dimension of
.
The dimension of
![]() is t+1. Let us emphasize that the degree of
chordal rings is 2t in general, except whenever there is a chord of
length n/2. In this case n is even and the degree is 2t-1.
is t+1. Let us emphasize that the degree of
chordal rings is 2t in general, except whenever there is a chord of
length n/2. In this case n is even and the degree is 2t-1.
![\begin{theorem}[\cite{NO97}]\mbox{}
\beginsmall{itemize}
\par\item For every $l ...
...D$\ is the diameter of $\mbox{$\cC$}(n;l)$.
\par\endsmall{itemize}
\end{theorem}](img175.gif)
A ``natural'' labeling of the nodes for chordal rings is the cyclic
labeling: Consecutive labeling of nodes around the ring. This labeling
is not always the best possible one. For instance, [KL95] showed
that
![]() has no shortest path 1-IRS with cyclic labeling
whereas it is of compactness 1. In fact it is possible to
characterize graphs supporting a shortest path 1-IRS according a
cyclic labeling of nodes.
has no shortest path 1-IRS with cyclic labeling
whereas it is of compactness 1. In fact it is possible to
characterize graphs supporting a shortest path 1-IRS according a
cyclic labeling of nodes.
By the use of the Ádám property, [Man98] showed that
![]() is isomorphic to
is isomorphic to
![]() if and only if
if and only if
![]() .
For instance
.
For instance
![]() ,
which has no shortest path 1-IRS with
cyclic labeling (cf. [KL95]), is isomorphic to
,
which has no shortest path 1-IRS with
cyclic labeling (cf. [KL95]), is isomorphic to
![]() which
satisfies Theorem 26. Therefore,
which
satisfies Theorem 26. Therefore,
![]() .
.
![]()
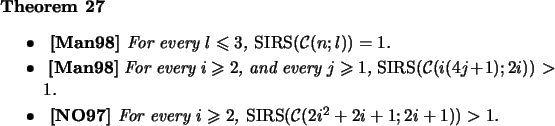
Let
![]() .
Since
.
Since ![]() is of diameter i
(cf. [BCH95]), it follows that 1-
is of diameter i
(cf. [BCH95]), it follows that 1-
![]() ,
for
every
,
for
every ![]() .
(Actually,
.
(Actually, ![]() is the chordal ring of degree 4
with the largest number of nodes for a given diameter). Moreover,
in [NO97], it is shown that 1-
is the chordal ring of degree 4
with the largest number of nodes for a given diameter). Moreover,
in [NO97], it is shown that 1-
![]() .
Also, the
smallest chordal ring known to be of compactness greater than 1 is
.
Also, the
smallest chordal ring known to be of compactness greater than 1 is
![]() ,
and 1-
,
and 1-
![]() .
[NO97] showed that
there exists some chordal rings,
.
[NO97] showed that
there exists some chordal rings, ![]() ,
where every shortest path
IRS using a cyclic labeling requires
,
where every shortest path
IRS using a cyclic labeling requires ![]() intervals, and also
that
intervals, and also
that
![]() has no shortest path 1-IRS of stretch factor
has no shortest path 1-IRS of stretch factor ![]() with a cyclic labeling. Other results about directed chordal rings
are mentioned in [KL95].
with a cyclic labeling. Other results about directed chordal rings
are mentioned in [KL95].
For two chords we have:
![\begin{theorem}[\cite{FGS94a}]
Let $i,j$\ be two integers, and $C = \mbox{$\cC$}...
...$-$\mbox{\rm stretch}(C) \leqs (j - i + 2)/2$.
\endsmall{itemize}
\end{theorem}](img196.gif)
And for higher dimensions,
![\begin{theorem}[\cite{FGS94a}]\mbox{}
\beginsmall{itemize}
\item For every $i \g...
...\mbox{$\cC$}(r^p;
r^{l_1},\ldots,r^{l_t}))=1$. \endsmall{itemize}
\end{theorem}](img197.gif)
The latter result can be easily generalized to
![]() when
when
![]() ,
and
,
and
![]() for every i.
for every i.
In [FGS94] is presented several results concerning IRS without the disjointness property of the labels assigned to the arcs, i.e., with Condition 2b of Definition 1 relaxed. See Paragraph 4.3 for a discussion of these results.
Note also that most of the results extend to circulant graphs in general, i.e., does not need to specify the chord of length 1.