
Questionnaire de compréhension immédiate
Répondez aux propositions suivantes par « VRAI » ou par « FAUX ».
Proposition 1 :
La simulation n'est qu'une façon empirique d'étude de files d'attente.
Proposition 2 :
Pour qu'une simulation produise une bonne approximation des paramètres du système étudié, il faut qu'un grand nombre d'événements soient simulés.
Proposition 3 :
La méthode de Monte Carlo permet de trouver la valeur exacte numérique d'une intégrale définie.
Proposition 4 :
On peut simuler le tirage d'une v.a. quelconque à partir du tirage d'une v.a. uniforme.
 |
Questionnaire à choix multiple
Question 1 :
Pour simuler les durées de service dans un système d'attente à un seul serveur, où la durée de service est constante :
Question 2 :
Pour générer une durée D qui peut prendre les valeurs 1, 2, 3, 4 avec les probabilités 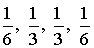 respectivement, on tire une v.a. u uniformément répartie sur
respectivement, on tire une v.a. u uniformément répartie sur 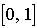 . Ensuite on pose :
. Ensuite on pose :
On considère un système d'attente à un seul serveur. Les interarrivées sont les v.a. indépendantes uniformément réparties sur l'intervalle 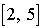 en mn. La durée du service est constante et vaut 3 mn. Une suite de 10 tirages uniformes dans
en mn. La durée du service est constante et vaut 3 mn. Une suite de 10 tirages uniformes dans 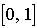 produit 0,3 0,7 0,2 0,8 0,5 0,6 0,3 0,2 0,9 0,1.
produit 0,3 0,7 0,2 0,8 0,5 0,6 0,3 0,2 0,9 0,1.
Transformer les tirages uniformes dans 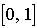 dans
dans 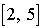 , qui seront considérés comme 10 interarrivées dans la suite.
, qui seront considérés comme 10 interarrivées dans la suite.
Dessiner la courbe de variation de 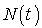 dans l'intervalle de temps
dans l'intervalle de temps 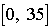 (en mn).
(en mn).
En déduire une estimation du nombre moyen d'usagers dans le système, du nombre moyen d'usagers dans la file d'attente, du temps moyen par usager passé dans le système et du temps moyen passé dans la file.
 |
 Consulter la solution... Consulter la solution... |
Une variable aléatoire X prend ses valeurs dans l'intervalle réel 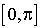 . Elle admet la densité :
. Elle admet la densité : 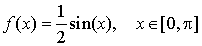 .
.
Décrire une méthode simulant un tirage de X à partir d'un tirage d'une v.a. uniforme dans 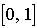 .
.
 |
 Consulter la solution... Consulter la solution... |
Ecrire une méthode de Monte Carlo pour estimer la valeur de 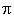 à partir de l'aire située entre les deux axes et portion de cercle d'équation
à partir de l'aire située entre les deux axes et portion de cercle d'équation 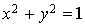 situé dans le premier quadrant du plan.
situé dans le premier quadrant du plan.
 |
 Consulter la solution... Consulter la solution... |