Proposition 1 :

Dans tous les processus de naissance et de mort la distribution de probabilité converge vers une distribution stationnaire qui ne dépend pas de l'état initial.

La réponse est non (Voir les conditions d'ergodicité : un processus est ergodique si tous ses états sont persistants positifs).

Proposition 2 :

Une condition nécessaire et suffisante pour que la distribution de probabilité tende vers une distribution stationnaire est que .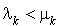

La réponse est non (Voir les conditions d'ergodicité).
 

Proposition 3 :

Dans un processus de naissance et de mort, si 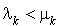à partir d'un certain rang, alors la distribution de probabilité tend vers une distribution stationnaire (processus ergodique).

La réponse est oui. En effet une condition suffisante pour l'ergodicité est que 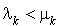à partir d'un certain rang.

Proposition 4 :

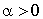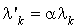Si dans un processus de naissance et de mort, on multiplie le taux de naissance et le taux de mort par la même constante (i.e. et 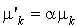), alors la nature du processus ne change pas.

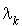La réponse est oui. En effet dans les conditions d'ergodicité, si l'on multiplie les et 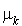par une même constante 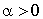, elles ne seront pas modifiées.