 La réponse est oui. En effet, si le taux d'arrivée du processus est
La réponse est oui. En effet, si le taux d'arrivée du processus est 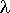 , l'interarrivée est une v.a. exponentielle d'espérance mathématique
, l'interarrivée est une v.a. exponentielle d'espérance mathématique 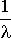 .
.Affirmation 1 :
L'espérance mathématique d'une interarrivée est l'inverse du taux d'arrivée du processus de Poisson associé.
 La réponse est oui. En effet, si le taux d'arrivée du processus est
La réponse est oui. En effet, si le taux d'arrivée du processus est 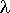 , l'interarrivée est une v.a. exponentielle d'espérance mathématique
, l'interarrivée est une v.a. exponentielle d'espérance mathématique 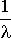 .
.
Affirmation 2 :
Dans un processus de Poisson, si on double le taux d'arrivée, l'interarivée sera divisée par 2.
 La réponse est non. L'interarrivée est une v.a. qui prend une valeur avec certaine probabilité. Elle ne sera donc pas nécessairement divisée par 2.
La réponse est non. L'interarrivée est une v.a. qui prend une valeur avec certaine probabilité. Elle ne sera donc pas nécessairement divisée par 2.
Affirmation 3 :
Dans un processus de Poisson, si on double le taux d'arrivée, l'espérance mathématique de l'interarrivée sera divisée par 2.
 La résponse est oui (voir la question 1).
La résponse est oui (voir la question 1).
Affirmation 4 :
Si le processus d'arrivée d'usagers dans un établissement de services est un processus de Poisson de taux de 15 à l'heure, la durée moyenne de l'intervalle de temps entre deux arrivées consécutives est de 4 mn.
 La résponse est oui (voir la question 1).
La résponse est oui (voir la question 1).
Affirmation 5 :
On suppose que le processus d'arrivée de taxis est un processus de Poisson. Un usager qui attend depuis 10 minutes l'arrivée d'un taxi a plus de chance dans les 5 minutes qu'un autre qui vient de joindre une station similaire.
 La réponse est non. En effet, la durée d'attente suit une loi exponentielle et cette loi est sans mémoire. (cf. le cours).
La réponse est non. En effet, la durée d'attente suit une loi exponentielle et cette loi est sans mémoire. (cf. le cours).
 |