Module C1.7 : Processus stochastique et simulation
Qu'est-ce qu'une chaîne de Markov ?
Questionnaire à choix multiple

Question 1 :

Dans l'exercice sur le facteur et la boîte à lettres, les deux états correspondait à une boîte vide ou pleine (dans cet ordre) et la matrice de probabilités transitions était .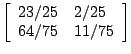

  1. Si dans une semaine la boîte est vide (avant le passage du facteur) lundi matin quelle est la probabilité qu'elle sera vide aussi mercredi?

      

      $(2/25)(64/75)$

      $(23/25)(23/25)+(2/25)(64/75)$

  2. Si dans une semaine la boîte est vide (avant le passage du facteur) lundi matin et encore mercredi matin, quelle est la probabilité qu'elle était vide aussi mardi?

      

      $(2/25)(64/75)$

      $(23/25)(23/25)+(2/25)(64/75)$


Question 2 :

Répondez Vrai ou Faux : à chaque assertion

  1. Un état périodique est forcément persistant.

         

  2. Chaque chaîne finie contient au moins un état persistant.

         

  3. Si tout circuit d'un état X à X a longueur un multiple de k, alors X est périodique avec période k.

         

  4. Si, dans une chaîne de n états X est un état persistant et il existe un chemin de X à Y, alors il existe un chemin de Y à X de longueur inférieure à n.