Définition 1
Un processus stochastique est une famille de variables aléatoires
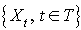
où t, représentant le temps, parcourt l'ensemble T.
Les valeurs de T peuvent être continues ou discrètes
Pour décrire un ensemble de phénomènes où le hasard intervient indépendamment de notre volonté, on introduit la notion de processus stochastique.
Définition 1 Un processus stochastique est une famille de variables aléatoires
où t, représentant le temps, parcourt l'ensemble T. Les valeurs de T peuvent être continues ou discrètes |
Exemples : la hauteur du niveau de la Garonne à un instant t, la valeur de mon portefeuille d'actions le soir à la clôture de la bourse de Paris. Notons que dans ce dernier exemple, le temps et les valeurs prises par la fonction aléatoire sont discrets alors que dans le premier exemples, les deux sont continus.
Une classe particulière de ces processus a été définie dans les années 30 par le mathématicien russe Markov.
On apellera état une valeur du processus stochastique prise à un instant t, et on apellera transition le passage d'un état à un autre.
Définition 2 Un processus est markovien, si pour tout instant u, pour toute valeur Les chaînes de Markov sont des processus markoviens qui évoluent dans le temps discret selon des transitions probabilistes. Elles vont donc décrire un ensemble de phénomènes aléatoires selon le principe des processus stochastiques. |
Propriété
La chaîne de Markov est associée à un ensemble d'états E possibles par lesquels le processus peut passer à un instant donné.
Remarque
Dans la suite de ce cours on travaillera sur un ensemble fini d'états.
Conséquence de la propriété markovienne
Nous ne considérons que des chaînes de Markov homogènes, c'est-à-dire que la probabilité de passage d'un état i à un état j de l'instant t à l'instant
Exemple 1 : Le jeu de Pile ou Face
Ce jeu se pratique à deux joueurs, un opposant et moi. Au début,
chaque joueur possède trois euros en pièces d'un euro. A chaque tour de
jeu, j'ai une probabilité p de gagner un euro et donc une probabilité
Voici une modélisation en chaîne de Markov de ce jeu:
L'ensemble E des états du système est
Cet ensemble est fini. Ces états correspondent au nombre d'euros que je peux posséder à tout instant du jeu.
Les transitions possibles entre chaque état peuvent être représentées comme suit :
Les transitions suivantes correspondent au gain de un euro.
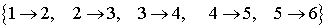
Les transitions suivantes correspondent à la perte de un euro.
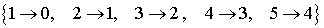
On introduit les transitions 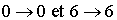 pour représenter le fait que le système ne change pas d'état. En général, on peut
avoir une possibilité de ne pas changer d'état à
un moment donné dans un état i ; cette possibilité est toujours representée par une possibilité de faire une "transition" de i à i.
pour représenter le fait que le système ne change pas d'état. En général, on peut
avoir une possibilité de ne pas changer d'état à
un moment donné dans un état i ; cette possibilité est toujours representée par une possibilité de faire une "transition" de i à i.
Exemple 2 : Une petite compagnie de livraison de colis
On considère une compagnie qui possède 4 camions utilisés pour des livraisons entre Bordeaux et Paris. Selon les demandes reçues chaque matin dans chaque ville, zéro, un ou plusieurs camions partent de Bordeaux et Paris pour arriver dans l'autre ville le soir. Si la demande dépasse le nombre de camions disponibles, ils partent tous mais les derniers clients restent dépourvus de service.
Pour un jour donné, soit 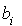 la probabilité d'une demande qui nécessite exactement i camions de Bordeaux vers Paris et
la probabilité d'une demande qui nécessite exactement i camions de Bordeaux vers Paris et 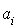 la même probabilité dans la direction inverse. On suppose que les
demandes dans les 2 villes sont indépendantes. Il y a 5 états selon le
nombre de camions à Bordeaux (la nuit).
la même probabilité dans la direction inverse. On suppose que les
demandes dans les 2 villes sont indépendantes. Il y a 5 états selon le
nombre de camions à Bordeaux (la nuit).
Probabilités de transition :
Il y a donc 25 probabilités de transition calculables.
Probabilité de transition de l'état 0 vers l'état 0 :
Il n'y a aucun camion à Bordeaux le matin, Il ne doit pas y en avoir
le soir donc tous les camions sont restés à Paris. La demande à Paris
doit être nulle. La probabilité est donc 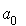 .
.
Probabilité de transition de l'état 0 vers l'état 1 :
Un seul camion parmi les 4 qui étaient à Paris est venu à Bordeaux. La probabilité est donc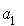 .
.
Probabilité de transition de l'état 1 vers l'état 0 :
Il y a 1 camion le matin à Bordeaux (et donc 3 à Paris), il faut
donc qu'il y ait à Bordeaux une demande supérieure ou égale à 1 camion
ET qu'en même temps il y ait une demande nulle à Paris. La probabilité
est donc :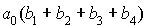 .
.
Probabilité de transition de l'état 1 vers l'état 1 :
Il y a 1 camion le matin à Bordeaux (et donc 3 à Paris), il faut
donc qu'il y ait (aucune demande à Bordeaux ET aucune demande à Paris)
OU (une demande supérieure ou égale à 1 à Bordeaux ET une demande exactement 1 à
Paris). La probabilité est donc : 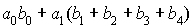
Voir l'exercice (ci-dessous) pour les autres probabilités.