Degré moyen

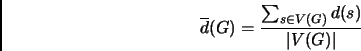
Selon la définition 5.2, le degré d'un sommet est égal au nombre de brins d'arêtes incidents au sommet. Ici, nous allons définir formellement le degré moyen d'un graphe.

Définition 9.1   Le degré moyen d'un graphe $G$, noté $\overline{d}(G)$, est défini par :

$$\overline{d}(G) = \frac{\sum_{s \in V(G)} d(s)}{\vert V(G)\vert}$$

L'objectif de cette section est de trouver différents algorithmes pour calculer le degré moyen.

Pour le type abstrait centré-arêtes, le travail est presque trivial. On applique directement le théorème 5.1, qui nous donne $\sum_{s \in V(G)} d(s)$ en fonction de $\vert E(G)\vert$, puis on divise par $\vert V(G)\vert$.

Voici l'algorithme sous une forme plus ``algorithmique'' :

Algorithme 9.1    
Entrée : un graphe $G$ utilisant le type abstrait centré-arêtes
Sortie : le degré moyen de $G$
Algorithme :

1. utiliser l'opération NB_EDGES(G) pour calculer le nombre d'arêtes $\vert E(G)\vert$,
2. multiplier par $2$ pour obtenir le nombre de brins d'arêtes de $G$,
3. utiliser l'opération NB_NODES(G) pour calculer le nombre de sommets $V(G)$,
4. diviser $2\vert E(G)\vert$ par $\vert V(G)\vert$ et renvoyer le résultat.

Cet algorithme est particulièrement simple. Il ne contient ni boucle, ni test. En fait, son temps d'exécution est constant, indépendant de la taille (i.e., du nombre de sommets et du nombre d'arêtes) du graphe. Dans ce cas, on dit que la complexité asymptotique est $O(1)$. Cela signifie que la forme générale de la fonction du temps de cet algorithme est la même que celle de la fonction constante $f(n)$ dont la valeur est $1$ pour toute valeur de $n$. Un algorithme de complexité $O(1)$ est optimal. Nous avons donc trouvé le meilleur algorithme pour calculer le degré moyen d'un graphe. Malheureusement, cet algorithme n'est utilisable que dans le cas centré-arêtes.

Si le type abstrait est centré-sommets, nous sommes obligés d'examiner chaque sommet pour déterminer le nombre de brins d'arêtes incidents à ce sommet. Voici un algorithme possible :

Algorithme 9.2    
Entrée : un graphe $G$ utilisant le type abstrait centré-sommets
Sortie : le degré moyen de $G$
Algorithme :

1. utiliser l'opération NB_NODES(G) pour calculer le nombre de sommets $\vert V(G)\vert$,
2. initialiser un accumulateur à $0$,
3. pour $i$ allant de $0$ à $\vert V(G)\vert - 1$, faire
   1. utiliser l'opération NODE(G, i) pour récupérer le sommet numéro $i$ du graphe,
   2. utiliser l'opération NB_EDGES(s) pour récupérer le degré du sommet,
   3. additionner ce degré à l'accumulateur,
4. diviser l'accumulateur par $\vert V(G)\vert$ et renvoyer le résultat.

Cet algorithme contient une boucle qui est exécutée une fois pour chacun des sommets du graphe. Le corps de la boucle ne contient que des opérations élémentaires. Cela donne une complexité asymptotique $O(\vert V(G)\vert)$. Autrement dit, l'algorithme prend un temps d'exécution proportionnel au nombre de sommets du graphe. On dit aussi qu'un tel algorithme est linéaire ou qu'il a une complexité linéaire. Dans notre cas, il faut préciser qu'il est linéaire par rapport au nombre de sommets du graphe.

Le temps d'exécution d'un algorithme dépend donc du type abstrait, i.e., des opérations élémentaires disponibles. Dans le cas du type abstrait centré-arêtes, on a un algorithme de complexité $O(1)$, alors que dans le cas du type abstrait centré-sommets, on a un algorithme de complexité $O(\vert V(G)\vert)$. Mais attention à ne pas conclure qu'un des types abstraits est meilleur que l'autre. Pour d'autres problèmes les performances sont inversées.