Complexity of Characterization

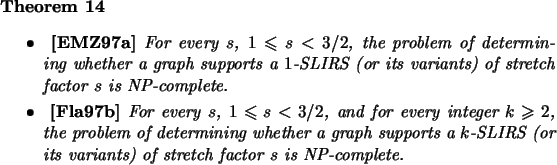
The characterization of IRS with at most 1 interval per arc (linear or cyclic) is polynomial if there is no constraint about the path lengths induced by the routing, see Paragraph 2.4. The problem becomes much harder when, for example, the shortest paths are required. Because the labeling can be optimized over all the possible node- and arc-labeling (including all the possible choice of routing paths), it appears that determining whether or not a graph has a shortest path 1-IRS is difficult in practice. The best-known NP-completeness results are the following:

$\begin{theorem} \mbox{} \beginsmall{itemize} \item~{\bf\cite{EMZ97a}} For every... ...riants) of stretch factor $s$\ is NP-complete. \endsmall{itemize} \end{theorem}$

Thus it is NP-complete for the case of weighted graphs (NP-completeness results are stated for the unweighted case), and shortest path IRS (s = 1). The result concerning the stretch factor was not mentioned in the original paper of [Fla97b]. However, since their construction is a graph of diameter 2, is quite easy to see that G has a shortest path 1-SLIRS (or its variant) if and only if G has a 1-SLIRS of stretch factor s < 3/2.

In [FGS95] it is also mentioned that the problem of determining the minimum K such that a given weighted graph supports a shortest path IRS with a total number of K intervals, for the entire graph, is NP-hard.

Open question 4
- Does the characterization of graphs supporting shortest path 1-SLIRS (and its variants) NP-complete when restricted to planar graphs?
- What is the best polynomial time approximation algorithm for the problem of characterization of graphs supporting a shortest path 1-SLIRS (and its variants)? Note that Theorem 14 implies that no polynomial time approximation algorithm can exist with a ratio less than 2 on the compactness of a graph.
- Does the following problem remain NP-hard: Find the smallest k such that k- $\mbox{\rm stretch}(G) \leqs s$ , for some $s \geqs 3/2$ ? or k- $\mbox{\rm dilation}(G) \leqs \delta$ , for some $\delta$ ?

In Paragraph 4.1 we will see that the problem becomes polynomial under some assumptions of non uniform link costs (dynamic link-costs).

The general problem of shortest path k-IRS is difficult to solve, however shortest path k-IRS have been found for many large classes of graphs.