Logic expressions

Introduction

To define what a combinatorial circuit does, we can use a logic expression or an expression for short. Such an expression uses the two constants 0 and 1, variables such as x, y, and z (sometimes with suffixes) as names of inputs and outputs, and the operators + (which stands for or), * (which stands for and, and is usually replaced as usual with juxtaposition), and a horizontal bar (which stands for not). As usual, multiplication is considered to have higher priority than addition. Parentheses are used to modify the priority.

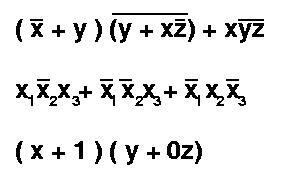
Examples:

Correspondence between expressions and combinatorial circuits

Each expression has a trivial corresponding combinatorial circuit. For instance, the expressions in the example above, correspond to the following circuits:

Power of logic expressions

A valid question is: can logic expressions describe all possible combinatorial circuits?. The answer is yes and here is why:

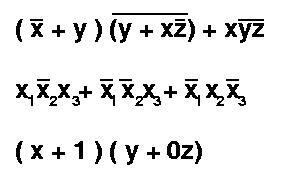
You can trivially convert the truth table for an arbitrary circuit into an expression. The expression will be in the form of a sum of products of variables and there inverses. Each row with output value of 1 of the truth table corresponds to one term in the sum. In such a term, a variable having a 1 in the truth table will be uninverted, and a variable having a 0 in the truth table will be inverted.

Take the following truth table for example:

  x y z | f
  ---------
  0 0 0 | 0
  0 0 1 | 0
  0 1 0 | 1
  0 1 1 | 0
  1 0 0 | 1
  1 0 1 | 0
  1 1 0 | 0
  1 1 1 | 1
The corresponding expression is:

Since you can describe any combinatorial circuit with a truth table, and you can describe any truth table with an expression, you can describe any combinatorial circuit with an expression.

Simplicity of logic expressions

There are many logic expressions (and therefore many circuits) that correspond to a certain truth table, and therefore to a certain function computed. For instance, the following two expressions compute the same function:

The left one requires two gates, one and-gate and one or-gate. The second expression requires two and-gates and one or-gate. It seems obvious that the first one is preferable to the second one. However, this is not always the case. It is not always true that the number of gates is the only way, nor even the best way, to determine simplicity.

We have, for instance, assumed that gates are ideal. In reality, the signal takes some time to propagate through a gate. We call this time the gate delay. We might be interested in circuits that minimize the total gate delay, in other words, circuits that make the signal traverse the fewest possible gates from input to output. Such circuits are not necessarily the same ones that require the smallest number of gates.