Tris récursifs

var T:tableau[1..N] d'entiers;

• Tri fusion
  
• Tri rapide
  

Tri fusion

Cet algorithme consiste à diviser la séquence d'entiers en deux sous-séquences, à les trier de manière récursive, puis à fusionner les deux sous-séquences triées. On utilise la fonction fusion vue au chapitre tris non récursifs

fonction triFusion(ref T:tableau[1..N]d'entiers):vide;
  var d,f:entier;
  fonction fusionLocal(ref T:tableau[1..N] d'entier;
                          val d,m,f:entier):vide;
    var C:tableau[1..f-d+1]d'entier;
    début
       C:=fusion(T,T,d,m,m+1,f);
       copie(C,T,d,f,d);
    fin
  finfonction
  fonction triFusionRec(ref T:tableau[1..N]d'entiers; val d,f:entier):vide;
    début
      si d<f alors
        m=partieEntiere((d+f)/2);
        triFusionRec(T,d,m);
        triFusionRec(T,m+1,f);
        fusionLocal(T,d,m,f);
      finsi
    fin
  finfonction 
  début
    trifusionRec(T,1,N)
  fin
finfonction

On a le déroulement ici
Propriété 9.1. La complexité du tri fusion pour une séquence de n éléments est O(nlog₂(n)).

idée de la preuve La complexité de la fonction triFusion est donnée par la complexité de triFusionRec. Soit f(n) le nombre de test effectué par cette fonction. On a

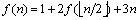
f(1)=0.
Soit p tel que 2^p≤n≤ 2^p+1. On a donc p≤log₂(n)≤ p+1.
On en déduit



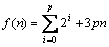
et



---

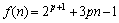
Tri rapide


Cet algorithme consiste à utiliser une valeur x de la séquence pour diviser la séquence d'entiers en deux sous-séquences:
• l'ensemble des valeurs inférieures ou égales à x
• l'ensemble des valeurs supérieures à x.
Puis la procédure s'effectue récursivement sur les deux sous séquences.

fonction triRapide(ref T:tableau[1..N]d'entiers):vide;
  fonction diviserSequence(ref T:tableau[1..N] d'entier;
                          val d,f:entier):entier;
    var x,i:entier;
    début
      x=T[f];
      i=d-1;
      pour j allant de d à f-1 faire
        si T[j]≤x alors
          i=i+1;
          echanger(T,i,j);
        finsi
      finpour
      echanger(T,i+1,f);
      retourner(i+1);
    fin
  finfonction
  fonction triRapideRec(ref T:tableau[1..N]d'entiers; val d,f:entier):vide;
    var p:entier;
    début
      si d<f alors
        p=diviserSequence(T,d,f);
        triRapideRec(T,d,p-1);
        triRapideRec(T,p+1,f);
      finsi
    fin
  finfonction 
  début
    triRapideRec(T,1,N)
  fin
finfonction

On a le déroulement ici


Propriété 9.2. La complexité du tri rapide pour une séquence de n éléments est

• au maximum en O(n²),
• en moyenne et au minimum en O(nlog(n)).