table des matières
Université Bordeaux 1
Licence Semestre 2   Initiation à l'algorithmique
Dernière mise à jour effectuée le 2 Juillet 2007

Structures de données

  1. Définition

    2. Définition 3.1. Une séquence sur un ensemble E est une suite d'éléments (e1,e2,...en) d'éléments de E.
    Une séquence peut contenir des éléments identiques de l'ensemble E.
    Exemple 3.1
    (3,5,8,2,12,6) est une séquence d'éléments de N, ensemble des entiers naturels.
    ("a","z","T","A","a") est une séquence sur l'ensemble des caractères imprimables(char).
    Il existe plusieurs variantes de séquences suivant les opérations de manipulation autorisées : accès par l'indice de l'élément ou non, accès à la fin de la séquences ou non, ....
    On utilisera en général des noms particuliers dépendants des caractéristiques de la séquence.
    Exemple 3.2
    Un vecteur peut être défini par une séquence dans laquelle l'accès aux éléments se fait par son indice et la taille de la séquence dépend de l'espace dans lequel on se trouve. On dit aussi qu'on a un accès direct à l'élément. Dans la plupart des langages de programmation, le vecteur existe sous le nom d'array.
    Exemple 3.3
    Soit la procédure calculant la factorielle 
    fonction fac(val n:entier):entier;
  begin
  if n<=1 alors 
    retourner(1)
  sinon
    retourner(n*fac(n-1))
  finsi
finfonction
Programme Python
    La séquence des valeurs de n au cours des appels récursifs doit être mémorisée. Supposons l'appel fac(4) alors
    • il y aura appel de fac(3), la mémorisation de n se fera par la séquence L=(4)
    • il y aura appel de fac(2), la mémorisation de n se fera par la séquence L=(3,4)
    • il y aura appel de fac(1), la mémorisation de n se fera par la séquence L=(2,3,4)
    • après exécution de fac(1), et la valeur est supprimée en tete de séquence L=(3,4)
    • après exécution de fac(2), n prend pour valeur la tête de la séquence et la valeur est supprimée en tete de séquence L=(4)
    • après exécution de fac(3), n prend pour valeur la tête de la séquence et la valeur est supprimée en tete de séquence L=()

  2. Structure

    3. Soient F1,F2,... ,Fp des ensembles.
    Définition 3.2. Une structure sur F1xF2x...xFp est une séquence (f1,f2,...fk) telle que
    Les structures sont des cas particuliers de séquences. En algorithmique, chaque ensemble Fi peut être un type de base ou une structure. ce mécanisme permet de définir de nouveaux types plus complexes que les types de base.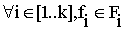
    En EXALGO, on écrit 
    nom_du_type=structure
              nom_champs_1:type1;
              nom_champs_2:type2;
              .......
              nom_champs_k:typek;
            finstructure.
    Ceci signifie que lorsqu'une variable est déclarée de ce type, elle référence k variables en même temps. Soit V une variable dont le type est une structure, on désigne un des champs par V. suivi du nom du champs.
    Exemple 3.4
    Une date de naissance est un exemple de structure. On peut ecrire : 
    dateDeNaissance=structure
                  jourDeNaissance:entier;
                  moisDeNaissance:entier;
                  annéeDeNaissance:entier;
                finstructure.
    On peut définir une structure composée du sexe et de la date de naissance 
    individu=structure
           sexe:booléen
           date:dateDeNaissance;
         finstructure.
    Soit la déclaration 
    var I:individu
    alors I.sexe sera un booléen et I.date.jourDeNaissance sera un entier.
    Ainsi les instructions suivantes ont un sens: 
    I.date.jour=12;
I.sexe=false;

  3. Table d'association à clé unique

    4. Définition 3.3 Soit F un ensemble. Une table d'association à clé unique est une séquence d'éléments de NxF (N est l'ensemble des entiers naturels), ((c1,f1),(c2,f2),...,(ck,fk)) telle que
    Les tables d'association sont un cas particulier de séquence d'éléments structurés. La structure se décrit en EXALGO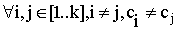 
    association=structure
          cle:entier;
          valeur:type_prédéfini;
finstructure
    Exemple 3.5
    Lors de l'activation du compte électronique, l'étudiant de l'Université Bordeaux 1 fournit un numéro INE qui sera associé à un mot de passe. On a donc quelque part dans le système de gestion des comptes une table d'association à index unique dont l'élément de séquence est : 
    Etudiant=structure
           INE:entier;
           motDePasse:typeMotDePasse;
finstructure